Lesson Solving typical problems on trigonometric equations

Algebra ->  Trigonometry-basics -> Lesson Solving typical problems on trigonometric equations      Log On


   

This Lesson (Solving typical problems on trigonometric equations) was created by by ikleyn(52781) About Me : View Source, Show
About ikleyn:

Solving typical problems on trigonometric equations


In this lesson you will find the solutions of these typical trigonometric equations:

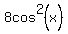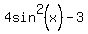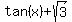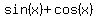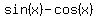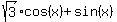    1.  8cos%5E2%28x%29 = 2.       2.  4sin%5E2%28x%29+-3 = 0.       3.  tan%28x%29+%2B+sqrt%283%29 = sec%28x%29.       4.  sin%28x%29+%2B+cos%28x%29 = -1.       5.  sin%28x%29+-+cos%28x%29 = sqrt%282%29.       6.  sqrt%283%29%2Acos%28x%29+%2B+sin%28x%29 = 1.

Problem 1

Solve an equation 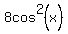  8cos%5E2%28x%29 = 2  in the interval [0,2pi)

Solution 

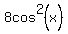8cos%5E2%28x%29 = 2  --->

cos^2(x) = 2%2F8 = 1%2F4,

cos(x) = +/-sqrt%281%2F4%29 = +/-1%2F2.

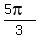cos(x) = 1%2F2  --->  x = pi%2F3  or/and  x = %285pi%29%2F3.

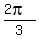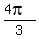cos(x) = -1%2F2  --->  x = %282pi%29%2F3   or/and  x = %284pi%29%2F3.

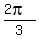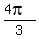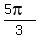Answer. x = pi%2F3, %282pi%29%2F3, %284pi%29%2F3 and %285pi%29%2F3.

Problem 2

Solve an equation 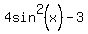  4sin%5E2%28x%29+-3 = 0  in the following domain  0 <= x < 2pi.

Solution


Problem 3

Solve an equation 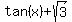  tan%28x%29+%2B+sqrt%283%29 = sec%28x%29.

Solution 

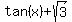tan%28x%29+%2B+sqrt%283%29 = sec(x)

is the same as

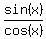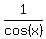sin%28x%29%2Fcos%28x%29 + sqrt%283%29 = 1%2Fcos%28x%29.

Multiply both sides by cos(x). You will get

sin%28x%29 + sqrt%283%29%2Acos%28x%29 = 1.


Multiply both sides by 1%2F2. You will get

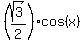%281%2F2%29%2Asin%28x%29 + %28sqrt%283%29%2F2%29%2Acos%28x%29 = 1%2F2.


Recall that 1%2F2 = cos%28pi%2F3%29,  sqrt%283%29%2F2 = sin%28pi%2F3%29.

Therefore, you can write the last equation as 

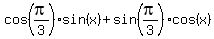cos%28pi%2F3%29%2Asin%28x%29+%2B+sin%28pi%2F3%29%2Acos%28x%29 = 1%2F2.


Apply the addition formula for sine.  ( It is cos(a)*sin(b) + sin(a)*cos(b) = sin(a+b). 
                                        See the lesson Addition and subtraction formulas in this site ). You will get

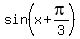sin%28x+%2B+pi%2F3%29 = 1%2F2.

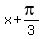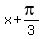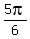It implies  x+%2B+pi%2F3 = pi%2F6  or  x+%2B+pi%2F3 = 5pi%2F6.

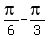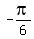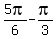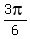Hence,  x = pi%2F6-pi%2F3 = -pi%2F6  or  x = 5pi%2F6-pi%2F3 = 3pi%2F6 = pi%2F2.

The last root doesn't fit due to "sec" in the original equation.


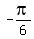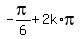Answer.  x = -pi%2F6,  or  -pi%2F6+%2B+2k%2Api for any integer "k".

Problem 4

Solve for x: 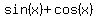  sin%28x%29+%2B+cos%28x%29 = -1.

Solution 

sin(x) + cos(x) = -1.    (1)   (It is the original equation)

Square its both sides. You will get

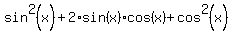sin%5E2%28x%29+%2B+2%2Asin%28x%29%2Acos%28x%29+%2B+cos%5E2%28x%29 = 1.   (2)

From the other side, there is an identity

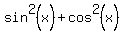sin%5E2%28x%29+%2B+cos%5E2%28x%29 == 1.   (3)

Comparing (2) and (3), you get

2*sin(x)*cos(x) = 0,   or  sin(x)*cos(x) = 0.    (4)

Equation (4) splits in two independent equations


1)  sin(x) = 0  --->  x = k%2Api,   k = 0. +/-1. +/-2, . . .           (5)


2)  cos(x) = 0  --->  x = pi%2F2+%2B+k%2Api,   k = 0. +/-1. +/-2, . . .    (6)


Now we should check which of the found values (5), (6) satisfy the original equation.

Of the set (5), all x satisfy sin(x) = 0. Hence, only those of (5) satisfy the original equation where cos(x) = -1.
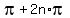They are  x = pi+%2B+2n%2Api,    n = 0, +/-1. +/-2, . . . ,  or 

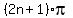          x = %282n%2B1%29%2Api,  n = 0, +/-1. +/-2, . . . ,                 (5').

Of the set (6), all x satisfy cos(x) = 0. Hence, only those of (6) satisfy the original equation where sin(x) = -1.
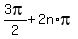They are  x = 3pi%2F2+%2B+2n%2Api,   n = 0, +/-1. +/-2, . . . ,  or 

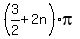          x = %283%2F2+%2B+2n%29%2Api,  n = 0, +/-1. +/-2, . . . ,             (6'). 

Answer.  The union of the sets (5') and (6') is the solution of the original equation.

Problem 5

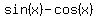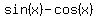Solve an equation   sin%28x%29+-+cos%28x%29 = sqrt%282%29.

Solution 

sin%28x%29+-+cos%28x%29 = sqrt%282%29.

Multiply both sides by sqrt%282%29%2F2. You will get

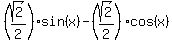%28sqrt%282%29%2F2%29%2Asin%28x%29+-+%28sqrt%282%29%2F2%29%2Acos%28x%29 = 1.             (1)

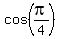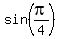Notice and use that sqrt%282%29%2F2 = cos%28pi%2F4%29 = sin%28pi%2F4%29.

Then from (1) you will get 

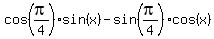cos%28pi%2F4%29%2Asin%28x%29+-+sin%28pi%2F4%29%2Acos%28x%29 = 1.       (2)

Now use the formula sin(a)*cos(b) - cos(a)*sin(b) = sin(a-b). Then from (2) you will get

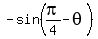-sin%28pi%2F4-theta%29 = 1.

It implies 

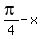pi%2F4+-+x = 3pi%2F2.

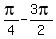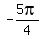Then x = pi%2F4+-+3pi%2F2 = -5pi%2F4.

It is the same as x = 3pi%2F4 in the interval 0 <= theta < 2pi.

The plot below confirms the solution ( 3pi%2F4 ~= 2.33 )



Plots y = 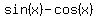sin%28x%29+-+cos%28x%29 and y = sqrt%282%29


Problem 6

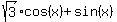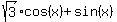Find the general solution to an equation   sqrt%283%29%2Acos%28x%29+%2B+sin%28x%29 = 1.

Solution 

sqrt%283%29%2Acos%28x%29+%2B+sin%28x%29 = 1.

Multiply both sides by 1%2F2. You will get

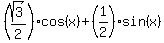%28sqrt%283%29%2F2%29%2Acos%28x%29+%2B+%281%2F2%29%2Asin%28x%29 = 1%2F2.           (1)

Notice that sqrt%283%29%2F2 = sin%28pi%2F3%29, 1%2F2 = cos%28pi%2F3%29. 

Substitute it into the left side of (1). You will get

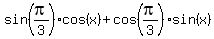sin%28pi%2F3%29%2Acos%28x%29+%2B+cos%28pi%2F3%29%2Asin%28x%29 = 1%2F2.    (2)

Apply the formula sin(a)*cos(b) + cos(a)*sin(b) = sin(a+b) to the left side of (2). You ill get

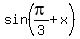sin%28pi%2F3+%2B+x%29 = 1%2F2.                       (3)

It implies 

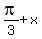pi%2F3+%2B+x = pi%2F6+%2B+2k%2Api,  k = 0, +/-1, +/-2, . . . or

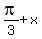pi%2F3+%2B+x = 5pi%2F6+%2B+2k%2Api,  k = 0, +/-1, +/-2, . . .


Thus there are two sets of solutions:

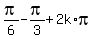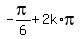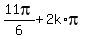1.  x = pi%2F6+-+pi%2F3+%2B+2k%2Api = -pi%2F6+%2B+2k%2Api,  which is equivalent to  x = 11pi%2F6+%2B+2k%2Api,


and the other family


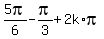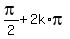2.  x = 5pi%2F6+-+pi%2F3+%2B+2k%2Api = pi%2F2+%2B+2k%2Api


Answer.  There are two sets of solutions:  1)  x = 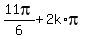11pi%2F6+%2B+2k%2Api  and  2)  x = 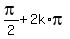pi%2F2+%2B+2k%2Api,  k = 0, +/-1, +/-2, . . .

The plot below confirms these solutions.



Plots y = 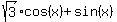sqrt%283%29%2Acos%28x%29+%2B+sin%28x%29 and y = 1


My other lessons on calculating trig functions and solving trig equations in this site are
    - Calculating trigonometric functions of angles
    - Advanced problems on calculating trigonometric functions of angles
    - Evaluating trigonometric expressions
    - Solve these trigonometry problems without using a calculator
    - Finding the slope of the bisector to the angle formed by two given lines in a coordinate plane

    - Solving simple problems on trigonometric equations
    - Solving more complicated problems on trigonometric equations
    - Solving advanced problems on trigonometric equations
    - Challenging problems on trigonometric equations
    - Miscellaneous problems on solving trigonometric equations
    - Solving twisted trigonometric equations
    - Truly elegant solution to one trigonometric equation
    - Non-standard Trigonometry problems

    - Proving Trigonometry identities
    - Calculating the sum  1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)

    - Find the height
    - Word problems on Trigonometric functions
    - Solving upper-league Trigonometry equations
    - Math OLYMPIAD level problems on Trigonometry
    - Trigonometry entertainment problems

    - OVERVIEW of lessons on calculating trig functions and solving trig equations

Use this file/link  ALGEBRA-II - YOUR ONLINE TEXTBOOK  to navigate over all topics and lessons of the online textbook  ALGEBRA-II.

This lesson has been accessed 1808 times.