Lesson Solving more complicated problems on trigonometric equations

Algebra ->  Trigonometry-basics -> Lesson Solving more complicated problems on trigonometric equations      Log On


   

This Lesson (Solving more complicated problems on trigonometric equations) was created by by ikleyn(52759) About Me : View Source, Show
About ikleyn:

Solving more complicated problems on trigonometric equations


In this lesson you will find the solutions of these trigonometric equations:

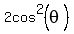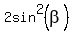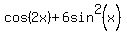      1.  2cos%5E2%28x%29+%2B+cos%28x%29 = 0.       2.  2sin%5E2%28x%29+-7sin%28x%29+%2B+3 = 0.       3.  2cos%5E2%28theta%29 = sin%28theta%29%2B1.       4.  3cos%28beta%29+%2B+3 = 2sin%5E2%28beta%29.       5.  cos%282x%29+%2B+6sin%5E2%28x%29 = 4.

Problem 1

Solve an equation   2cos%5E2%28x%29+%2B+cos%28x%29 = 0.

Solution 

2cos%5E2%28x%29+%2B+cos%28x%29 = 0.     (1)

Factor the left side. You will get

cos(x)*(2cos(x) + 1) = 0.

The last equation splits in two separate equations:

1.  cos(x) = 0  --->  x = pi%2F2  and/or  x = -pi%2F2.

    In the interval [0,2pi) there are no other solutions. 
    If you want to write general solution then  x = k%2Api, where k is any integer, k = 0, +/-1, +/-2 . . . 


2.  2cos(x) + 1 = 0  --->  cos(x) = -1%2F2  --->  x = 2pi%2F3  and/or  x = 4pi%2F3.

    In the interval [0,2pi) there are no other solutions.
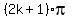    If you want to write a general solution, then  x = +/- pi%2F3 + %282k%2B1%29%2Api, where k is any integer, k = 0, +/-1, +/-2 . . . 

Answer. The solution of the original equation (1) is the union of the solutions to n.1 and n.2.

Problem 2

Solve an equation 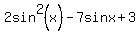2sin%5E2%28x%29+-+7sin+x+%2B+3 = 0 for all real values of x.

Solution 

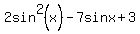2sin%5E2%28x%29+-+7+sin+x+%2B+3 = 0.

Group the terms to get factoring:

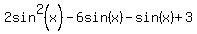2sin%5E2%28x%29+-+6sin%28x%29+-+sin%28x%29+%2B+3 = 0.

2sin%28x%29%2A%28sin%28x%29-3%29+-+%28sin%28x%29-3%29 = 0, 


(sin(x)-3)*(2sin(x)-1) = 0.


The last equation splits in two equations:


   1.  sin(x) = 3 (this equation has no solutions)

         or

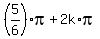   2.  sin(x) = 1/2  --->  x = pi%2F6+%2B+2k%2Api  or  x = %285%2F6%29pi+%2B+2k%2Api, where k is any integer k = 0, +/-1, +/-2, . . . 


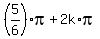Answer.  The solutions are  x = pi%2F6+%2B+2k%2Api  or  x = %285%2F6%29pi+%2B+2k%2Api, where k is any integer.

Problem 3

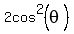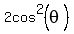Solve an equation   2cos%5E2%28theta%29 = sin%28theta%29%2B1.

Solution 

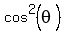2cos%5E2%28theta%29 = sin%28theta%29%2B1.

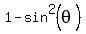Replace  cos%5E2%28theta%29  by  1+-+sin%5E2%28theta%29 to get the equation for sine only.  You will get

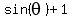2%2A%281-sin%5E2%28theta%29%29 = sin%28theta%29%2B1,   or

2+-+2sin%5E2%28theta%29 = sin%28theta%29%2B1,   or

2%2Asin%5E2%28theta%29+%2B+sin%28theta%29+-+1 = 0,   or  (after factoring left side)

%282%2Asin%28theta%29+-+1%29%2A%28sin%28theta%29+%2B+1%29 = 0.


The last equation splits in two equations:


   1.  2%2Asin%28theta%29+-+1 = 0  --->  sin%28theta%29 = 1%2F2  --->  theta = pi%2F6+%2B+2k%2Api  or  theta = 5pi%2F6+%2B+2k%2Api,  k = 0, +/-1, +/-2, . . . 


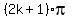   2.  sin%28theta%29+%2B+1 = 0  --->  sin%28theta%29 = -1  --->  theta = 3pi%2F4+%2B+2k%2Api = %282k%2B1%29%2Api,  k = 0, +/-1, +/-2, . . . 


Answer. The solution of the original equation is the union of the solutions to n.1 and n.2.

Problem 4

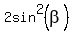Solve an equation   3cos%28beta%29+%2B+3 = 2sin%5E2%28beta%29.

Solution 

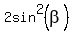3%2Acos%28beta%29+%2B+3 = 2sin%5E2%28beta%29.

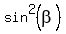Replace  sin%5E2%28beta%29  by  1+-+cos%5E2%28beta%29 to get the equation for cosine only.  You will get

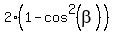3%2Acos%28beta%29+%2B+3 = 2%2A%281+-+cos%5E2%28beta%29%29,   or

3%2Acos%28beta%29+%2B+3 = 2+-+2%2Acos%5E2%28beta%29,   or

2%2Acos%5E2%28beta%29+%2B+3%2Acos%28beta%29+%2B+1 = 0,   or  (after factoring left side)

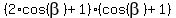%282%2Acos%28beta%29+%2B+1%29%2A%28cos%28beta%29+%2B+1%29 = 0.


It splits in two equations:


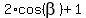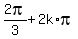   1.  2%2Acos%28beta%29+%2B+1 = 0  --->  cos%28beta%29 = -1%2F2  --->  beta = 2pi%2F3+%2B+2k%2Api  or  beta = 4pi%2F3+%2B+2k%2Api,  k = 0, +/-1, +/-2, . . . 


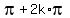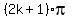   2.  cos%28beta%29+%2B+1 = 0  --->  cos%28beta%29 = -1  --->  beta = pi+%2B+2k%2Api = %282k%2B1%29%2Api,  k = 0, +/-1, +/-2, . . . 


Answer. The solution of the original equation is the union of the solutions to n.1 and n.2.

Problem 5

Solve an equation 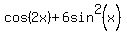  cos%282x%29+%2B+6sin%5E2%28x%29 = 4.

Solution 

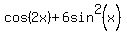cos%282x%29+%2B+6sin%5E2%28x%29 = 4.

The way to solve it is to transform the original equation into the equation for sine only.

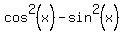To do it, use the formula for cosine of doubled argument cos(2x) = cos%5E2%28x%29+-+sin%5E2%28x%29
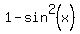and replace cos%5E2%28x%29 by 1-sin%5E2%28x%29. You will get cos(2x) = 1+-+2%2Asin%5E2%28x%29.
Now substitute it into original equation. You will get

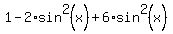1+-+2%2Asin%5E2%28x%29+%2B+6%2Asin%5E2%28x%29 = 4.

Collect like terms. You will get

4%2Asin%5E2%28x%29 = 3,   or

sin%5E2%28x%29 = 3%2F4,  or (after taking the square root from both sides)

sin(x) = +/- sqrt%283%29%2F2.

The solutions are x = pi%2F3, 2pi%2F3, 4pi%2F3, 5pi%2F3.

In the interval [0,2pi) these are all solutions.

If you want to write a general solution, then  x = +/- pi%2F3 + k%2Api,  where k is any integer, k = 0, +/-1, +/-2 . . .


My other lessons on calculating trig functions and solving trig equations in this site are
    - Calculating trigonometric functions of angles
    - Advanced problems on calculating trigonometric functions of angles
    - Evaluating trigonometric expressions
    - Solve these trigonometry problems without using a calculator
    - Finding the slope of the bisector to the angle formed by two given lines in a coordinate plane

    - Solving simple problems on trigonometric equations
    - Solving typical problems on trigonometric equations
    - Solving advanced problems on trigonometric equations
    - Challenging problems on trigonometric equations
    - Miscellaneous problems on solving trigonometric equations
    - Solving twisted trigonometric equations
    - Truly elegant solution to one trigonometric equation
    - Non-standard Trigonometry problems

    - Proving Trigonometry identities
    - Calculating the sum  1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)

    - Find the height
    - Word problems on Trigonometric functions
    - Solving upper-league Trigonometry equations
    - Math OLYMPIAD level problems on Trigonometry
    - Trigonometry entertainment problems

    - OVERVIEW of lessons on calculating trig functions and solving trig equations

Use this file/link  ALGEBRA-II - YOUR ONLINE TEXTBOOK  to navigate over all topics and lessons of the online textbook  ALGEBRA-II.

This lesson has been accessed 2372 times.