Challenging problems on trigonometric equations
In this lesson you will find the solutions of these trigonometric equations:
1. sin(x) + sin(2x) + sin(3x) = 0. 2. sin(x) + sin(3x) + sin(5x) = 0. 3. cos(x) + cos(2x) + cos(3x) + cos(4x) = 0. 4. sin(x) + sin(2x) + sin(3x) + sin(4x) = 0.
Problem 1
Solve an equation sin(x) + sin(2x) + sin(3x) = 0 over the interval [0,2pi).
Solution
sin(x) + sin(2x) + sin(3x) = 0. (1)
Apply the trigonometry formula  =
=  (see any serious textbook in trigonometry or the lessons
- FORMULAS FOR TRIGONOMETRIC FUNCTIONS
- Addition and subtraction of trigonometric functions
in this site) to the first and third addend in the left side of the original equation (1). You will get
(see any serious textbook in trigonometry or the lessons
- FORMULAS FOR TRIGONOMETRIC FUNCTIONS
- Addition and subtraction of trigonometric functions
in this site) to the first and third addend in the left side of the original equation (1). You will get
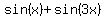 =
= 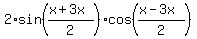 =
= 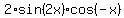 =
= 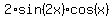 .
Now, the equation (1) takes the form
.
Now, the equation (1) takes the form
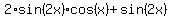 =
=  , or
, or
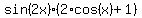 =
=  .
This equation deploys in two independent equations
1. sin(2x) = 0 ---> x =
.
This equation deploys in two independent equations
1. sin(2x) = 0 ---> x =  , x =
, x =  , k = 0, =/-1, +/-2. . . .
2. 2cos(x) + 1 = 0 ---> cos(x) =
, k = 0, =/-1, +/-2. . . .
2. 2cos(x) + 1 = 0 ---> cos(x) =  ---> x =
---> x = 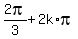 , x =
, x =  , k = 0, =/-1, +/-2. . . .
Answer. The solutions are a) x =
, k = 0, =/-1, +/-2. . . .
Answer. The solutions are a) x =  , x =
, x =  , k = 0, =/-1, +/-2. . . . and
b) x =
, k = 0, =/-1, +/-2. . . . and
b) x = 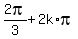 , x =
, x =  , k = 0, =/-1, +/-2. . . .
, k = 0, =/-1, +/-2. . . .
 Plot y = sin(x) + sin(2x) + sin(3x)
Plot y = sin(x) + sin(2x) + sin(3x)
Problem 2
Solve an equation sin(x) + sin(3x) + sin(5x) = 0 over the interval [0,2pi).
Solution
sin(x) + sin(3x) + sin(5x) = 0. (1)
Using the Trigonometry formula  , (*)
you can transform
, (*)
you can transform 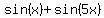 =
= 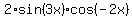 =
=  .
Then the left side of the given equation takes the form
.
Then the left side of the given equation takes the form
 =
=  +
+  =
= 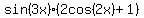 ,
and the equation (1) takes the form
,
and the equation (1) takes the form
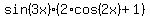 = 0. (2)
Equation (2) deploys in two independent equations:
1) sin(3x) = 0, which in the given interval has the solutions x = 0,
= 0. (2)
Equation (2) deploys in two independent equations:
1) sin(3x) = 0, which in the given interval has the solutions x = 0,  ,
,  ,
,  ,
,  , and
, and  .
2) 2*cos(2x) + 1 = 0, which is the same as cos(2x) =
.
2) 2*cos(2x) + 1 = 0, which is the same as cos(2x) =  .
In the given interval the last equation has the solutions
x =
.
In the given interval the last equation has the solutions
x =  ,
, 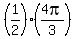 ,
,  ,
, 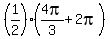 , or, which is the same,
x =
, or, which is the same,
x =  ,
,  ,
,  and
and  .
Answer. The solutions of the equation (1) in the interval [
.
Answer. The solutions of the equation (1) in the interval [ ,
, ) are x = 0,
) are x = 0,  ,
,  ,
,  ,
,  , and
, and  .
.
 Plot y = Sin(x) + Sin(3x) + Sin(5x)
Plot y = Sin(x) + Sin(3x) + Sin(5x)
Problem 3
Solve an equation cos(x) + cos(2x) + cos(3x) + cos(4x) = 0 over the interval [0,2pi).
Solution
cos(x) + cos(2x) + cos(3x) + cos(4x) = 0. (1)
Use the general formula of Trigonometry
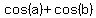 =
= 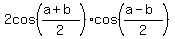 . (2)
You have
cos(x) + cos(4x) =
. (2)
You have
cos(x) + cos(4x) = 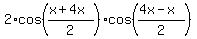 =
= 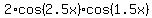 ,
cos(2x) + cos(3x) =
,
cos(2x) + cos(3x) = 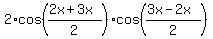 =
= 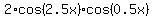 .
Therefore, the left side of the original equation is
cos(x) + cos(2x) + cos(3x) + cos(4x) = 2*cos(2.5x)*cos(1.5x) + 2*cos(2.5x)*cos(0.5x) = 2*cos(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*cos(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*cos(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Again, apply the formula (2) to the left side of (3). You will get an equivalent equation
.
Therefore, the left side of the original equation is
cos(x) + cos(2x) + cos(3x) + cos(4x) = 2*cos(2.5x)*cos(1.5x) + 2*cos(2.5x)*cos(0.5x) = 2*cos(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*cos(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*cos(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Again, apply the formula (2) to the left side of (3). You will get an equivalent equation
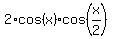 = 0. (4)
Equation (4) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =
= 0. (4)
Equation (4) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =  , k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 --->
, k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 --->  =
=  , k = 0, +/-1, +/-2, . . . , or
x =
, k = 0, +/-1, +/-2, . . . , or
x = 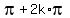 =
= 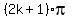 , k = 0, +/-1, +/-2, . . .
From (1) and (2), in the given interval the original equation has the roots
, k = 0, +/-1, +/-2, . . .
From (1) and (2), in the given interval the original equation has the roots  ,
,  ,
,  , or 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*cos(2.5x) ?
Of course, I must consider (and add to the solution set !) all the solutions of the equation
cos(2.5x) = 0.
They are 2.5x =
, or 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*cos(2.5x) ?
Of course, I must consider (and add to the solution set !) all the solutions of the equation
cos(2.5x) = 0.
They are 2.5x =  , k = 0, +/-1, +/-2, . . .
or, which is the same,
, k = 0, +/-1, +/-2, . . .
or, which is the same,
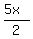 =
=  , k = 0, +/-1, +/-2, . . .
So, these additional solutions are x =
, k = 0, +/-1, +/-2, . . .
So, these additional solutions are x = 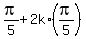 =
=  , k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions.
One family
, k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions.
One family  ,
,  ,
,  , or 90°, 180°, 270°.
The other family is
, or 90°, 180°, 270°.
The other family is 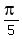 ,
, 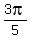 ,
,  =
=  ,
,  ,
, 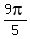 , or 36°, 108°, 180° (repeating root), 252°, 324°.
, or 36°, 108°, 180° (repeating root), 252°, 324°.
Solved.
CHECK
Look into the plot of the left side of the original equation
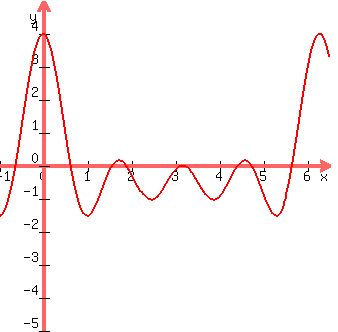 Plot y = cos(x) + cos(2x) + cos(3x) + cos(4x)
Do you see 7 roots in the interval [
Plot y = cos(x) + cos(2x) + cos(3x) + cos(4x)
Do you see 7 roots in the interval [ ,
, ) ?
) ?
Problem 4
Solve an equation sin(x) + sin(2x) + sin(3x) + sin(4x) = 0 over the interval [0,2pi).
Solution
sin(x) + sin(2x) + sin(3x) + sin(4x) = 0. (1)
Use the general formula of Trigonometry
 =
= 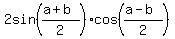 . (2)
You have
sin(x) + sin(4x) =
. (2)
You have
sin(x) + sin(4x) = 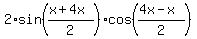 =
= 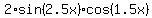 ,
sin(2x) + sin(3x) =
,
sin(2x) + sin(3x) = 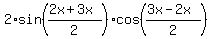 =
= 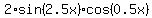 .
Therefore, the left side of the original equation is
sin(x) + sin(2x) + sin(3x) + sin(4x) = 2*sin(2.5x)*cos(1.5x) + 2*sin(2.5x)*cos(0.5x) = 2*sin(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*sin(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*sin(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Next, apply another general formula of Trigonometry
.
Therefore, the left side of the original equation is
sin(x) + sin(2x) + sin(3x) + sin(4x) = 2*sin(2.5x)*cos(1.5x) + 2*sin(2.5x)*cos(0.5x) = 2*sin(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*sin(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*sin(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Next, apply another general formula of Trigonometry
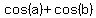 =
= 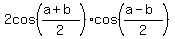 . (4)
Then the equation (3) becomes
. (4)
Then the equation (3) becomes
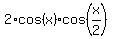 = 0. (5)
Equation (5) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =
= 0. (5)
Equation (5) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =  , k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 --->
, k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 --->  =
=  , k = 0, +/-1, +/-2, . . . , or
x =
, k = 0, +/-1, +/-2, . . . , or
x = 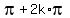 =
= 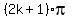 , k = 0, +/-1, +/-2, . . .
From (1) and (2), in the given interval the original equation has the roots
, k = 0, +/-1, +/-2, . . .
From (1) and (2), in the given interval the original equation has the roots  ,
,  ,
,  , or 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*sin(2.5x) ?
Of course, I must consider (and add to the solution set !) all the solutions of the equation
sin(2.5x) = 0.
They are 2.5x =
, or 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*sin(2.5x) ?
Of course, I must consider (and add to the solution set !) all the solutions of the equation
sin(2.5x) = 0.
They are 2.5x =  , k = 0, +/-1, +/-2, . . .
or, which is the same,
, k = 0, +/-1, +/-2, . . .
or, which is the same,
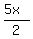 =
=  , k = 0, +/-1, +/-2, . . .
So, these additional solutions are x = 0,
, k = 0, +/-1, +/-2, . . .
So, these additional solutions are x = 0, 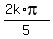 ,
, 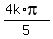 ,
, 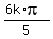 ,
, 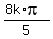 , k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions in the given interval.
One family is
, k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions in the given interval.
One family is  ,
,  , and
, and  , or 90°, 180° and 270°.
The other family is 0,
, or 90°, 180° and 270°.
The other family is 0, 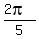 ,
, 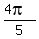 ,
, 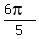 ,
,  , or 0°, 72°, 144°, 216°, 288°.
, or 0°, 72°, 144°, 216°, 288°.
Solved.
CHECK
Look into the plot of the left side of the original equation
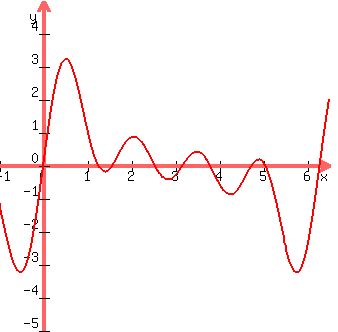 Plot y = sin(x) + sin(2x) + sin(3x) + sin(4x)
Do you see 8 roots in the interval [
Plot y = sin(x) + sin(2x) + sin(3x) + sin(4x)
Do you see 8 roots in the interval [ ,
, ) ?
) ?
My other lessons on calculating trig functions and solving trig equations in this site are
- Calculating trigonometric functions of angles
- Advanced problems on calculating trigonometric functions of angles
- Evaluating trigonometric expressions
- Solve these trigonometry problems without using a calculator
- Finding the slope of the bisector to the angle formed by two given lines in a coordinate plane
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
- Miscellaneous problems on solving trigonometric equations
- Solving twisted trigonometric equations
- Truly elegant solution to one trigonometric equation
- Non-standard Trigonometry problems
- Proving Trigonometry identities
- Calculating the sum 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)
- Find the height
- Word problems on Trigonometric functions
- Solving upper-league Trigonometry equations
- Math OLYMPIAD level problems on Trigonometry
- Trigonometry entertainment problems
- OVERVIEW of lessons on calculating trig functions and solving trig equations
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

