Questions on Geometry: Triangles answered by real tutors!

Tutors Answer Your Questions about Triangles (FREE)

Question 620349: http://img.geocaching.com/cache/large/8f671ade-1846-4e62-b2d7-2c73512ae1c8.gif
Three big one-inch squares (S3) are joined corner-to-corner to make an equilateral triangle. Inside that triangle, three little squares (S1) are fit into a similar shape. Finally, the line segment from the little square to the corner of the large triangle is used to form the medium square (S2) as shown.
-----(SEE IMAGE)-----
What is the ratio of areas of the medium square to the little square (S2:S1)?
Click here to see answer by KMST(5328)

Question 620498: Answer the following without the use of a calculator: SHow all working and give answers in surd or simplest form:
(sin60)/(sin45)(tan30)
Thank you! :)
Click here to see answer by lynnlo(4176)

Question 620505: Find the centroid of triangle EFG with vertices at E(-4, 1), F(2,3), and G(-4,-1). Thanks for the help.
Click here to see answer by ewatrrr(24785)

Question 620557: Recall that for triangle ABC the law of sines states that (sin A)/a= (sin B)/b= (sin C)/c. If angle A= 30, angle B= 45, and a= 16, find b.
A. Square root of 2
B. 4 times the square root of 2
C. the square root of 2 divided by 32
D. 16 times the square root of 2
I know the answer is D. but i do not know how to reach that solution.
Click here to see answer by jim_thompson5910(35256)

Question 620485: The angles of a triangle is a ratio of 3:6:9 find the angles?
Click here to see answer by Alan3354(69443)

Question 620598: The measures of the angles in a triangle are x, 2x, and 3x. The triangle is?

Click here to see answer by jim_thompson5910(35256)

Question 620598: The measures of the angles in a triangle are x, 2x, and 3x. The triangle is?

Click here to see answer by solver91311(24713)

Question 620765: triangle XYZ is a right triangle that is 30 60 90 If XY which is the shorter leg what is the hypotenuse
Click here to see answer by ewatrrr(24785)

Question 620842: the minute hand of a clock is 9cm long and the hour hand is two-thirds as long. How much farther than the tip of the hour hand will the tip of the minute hand move in one hour?
Click here to see answer by ankor@dixie-net.com(22740)

Question 621037: the perimeter of a right triangle is 90 ft. the ratio of the legs is 5:12. what is the length of the longest leg of the triangle?
Click here to see answer by matt501823(7)

Question 621082: One angle of an isosceles triangle is 16�. What are the other 2 angles?

Click here to see answer by vleith(2983)

Question 621181: Find the altitudes of a triangle whose side lengths are 13, 14, and 15
Click here to see answer by tomlaidlaw(14)

Question 621151: The second angle of a triangle is three times as large as the first. The third angle is 20 degrees less than the sum of the other two angles. Find the measure of the first angle.
Click here to see answer by tomlaidlaw(14)

Question 620263: A ladder is leaning against a house and is forming a 60 degree angle with the ground. If the top of the ladder is 15 from the ground, how long is the ladder to the nearest foot?
Click here to see answer by tomlaidlaw(14)

Question 616050: If you know only the sides of a triangle, For example, if a triangle had sides of 4 cm, 7 cm, and 12 cm, can you could not identify the three angles of that triangle. and likewise only knowing the three angles of some triangles to determine the other three sides, is that possible
Click here to see answer by tomlaidlaw(14)

Question 621531: in triangle DEF, e= 3.0 cm
angle F = 64
angle E 46
find the measurement of d
Click here to see answer by math-vortex(648)

Question 621688: A 15-foot ladder is leaning against a 30-foot wall. The bottom end of the ladder is 9 feet from the wall. How many feet above the ground does the ladder touch the wall?
Click here to see answer by ewatrrr(24785)

Question 621711: http://media.apexlearning.com/Images/200703/28/1248dd41-7b9c-438f-91f5-ffca7400a232.gif
What is the value of y?
Click here to see answer by ewatrrr(24785)

Question 621836: The perimeter of an equilateral triangle is 12 feet. what is the area?
Click here to see answer by rfer(16322)

Question 622003: the area of a triangle with sides of 6

Click here to see answer by ewatrrr(24785)

Question 622129: Which type of triangle will have it's incenter, orthocenter, Circumcenter and centroid at the same point?
Click here to see answer by solver91311(24713)

Question 622387: In a right angled triangle AB is hypotenuse.D,E and F are the mid-points of BC,AB and AC respectively.P,Q and R are the min-points of AD,CE and BF respectively.so prove that
((PA)^2 +(PB)^2 +(PC)^2)+((QA)^2 +(QB)^2 +(QC)^2)+((RA)^2 +(RB)^2 +(RC)^2)=(AB)^2
Click here to see answer by Edwin McCravy(20054)

Question 622441: They hypotenuse of a right triangle measures 8 meters and one of the legs measures 4 meters. Find the measure of the other leg (Round to the nearest hundredths when necessary).
Click here to see answer by rfer(16322)

Question 622706: the sides of a triangle have lengths of x, x+5, and 25. if the longest side is 25, which of the following values of x would make the right triangle?
Click here to see answer by ewatrrr(24785)

Question 622846: if the angle of the triangle is 70 , 3y-20 , and y+10 . . . what does y equal

Click here to see answer by ankor@dixie-net.com(22740)

Question 622981: Given: side b = 600, angle B = 11 degrees, angle C = 75degrees in triangle ABC; find side a and side c. (Round the answer to the nearest whole number.)
Click here to see answer by Alan3354(69443)

Question 622991: One angle of a rhombus measures 102 degrees, and the shorter diagonal is 4 inches long. How long is the side of the rhombus (to nearest whole number)?
Click here to see answer by mykasha(37)

Question 622993: A diagonal of a parallelogram is 50 inches long and makes angles of 37degrees10' and 49degrees20' with the sides. How long are the sides (to the nearest whole number)?
Click here to see answer by mykasha(37)

Question 623215: find the % increase in the area of the triangle if its each side is doubled
Click here to see answer by Alan3354(69443)

Question 623108: The measures of the angles of a triangle are given. List the sides from shortest to longest.
m∠r= 35 degrees, m∠s= 120 degrees, m∠t= 25 degrees
Click here to see answer by math-vortex(648)

Question 623349: The area of a rectangular wall in a classroom is 216 sq ft. Its length is 3 ft shorter than three times its width. Find the length and width of the wall of the classroom.
Click here to see answer by ewatrrr(24785)

Question 623408: hello there, I'm having trouble finding the lengths of this triangle whose measurements are as follows:
short leg=
long leg=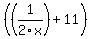
hypotenuse=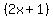
this is the work that I had done:

simplified:
written in standard form:
multiply everything by (11/4):
And now I'm stuck here, as you can see, there's no way I can factorize this, what have I done wrong?
Your help is very much appreciated.
Click here to see answer by Alan3354(69443)

Question 623601: Find a and b that a>0,b>0 and the point (a,b),(1,b) and (a,6) are vertices of a triangle of a base 3 units and area equal to 6 square units.
Click here to see answer by math-vortex(648)

Question 623716: The triangle ABC is a right, isosceles triangle. If the length of side AC is 3, give the lengths of the other two sides and the measures of angle A and angle B.

Click here to see answer by solver91311(24713)

Question 623697: In triangle ABC, side AC is extended through C to point D to create external angle BCD. Angle A measures 47 degrees and external angle BCD mesures 113 degrees. What is the measure of angle B?
Click here to see answer by ankor@dixie-net.com(22740)

Question 623863: In a right angled triangle besides the right angle one of the angles measure 30� what does the other angle measure

Click here to see answer by solver91311(24713)

Question 623908: find the measures of the angles of a triangle if the measures are in the ratio 2:3:4

Click here to see answer by solver91311(24713)

Question 623964: What happens when a triangle base is doubled but the height is cut in half how does it affect the area ,what if the height remains the same. I'm confused , Thank you
Click here to see answer by ewatrrr(24785)

Question 623976: Classify the triangle based on side lengths 4, 6 and 7.
Click here to see answer by ewatrrr(24785)

Question 624172: The height of a triangle is 4x + 5 inches and its base is equal to its height. Find its area.
Click here to see answer by math-vortex(648)

Question 624227: A triangle has sides measuring 5, 12, and 15 units. Find all the angles of the triangle to the nearest tenth of a degree.
I beleive it's a SSS Triangle
b^2=a^2=+C^2-2ac COS B
Cos B=12^2+15^2-5^2/2(12)(15) =144+225-25/360
=344/360
B=17.14
Sin A=12Sin17.14/5=0.7056
A=45
C117.9
Click here to see answer by Alan3354(69443)

Question 624359: Find the range for the measurement of the third side of a triangle, x, given the measures of the two sides: 3.8 ft and 9.2 ft.
Click here to see answer by ewatrrr(24785)

Question 624493: The hypotenuse of a right triangle is 5 inches. if one leg is 2 inches, find the degree measure of each angle
Click here to see answer by Theo(13342)

Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690