SOLUTION: Sketch ∆ABC with vertices: A(6,2) B(10,4) and C(-2,8) Label the midpoints of each side P, Q, and R respectively Algebraically find the centroid.

Algebra ->  Triangles -> SOLUTION: Sketch ∆ABC with vertices: A(6,2) B(10,4) and C(-2,8) Label the midpoints of each side P, Q, and R respectively Algebraically find the centroid.      Log On


   

Question 932035: Sketch ∆ABC with vertices:
A(6,2) B(10,4) and C(-2,8)
Label the midpoints of each side
P, Q, and R respectively
Algebraically find the centroid.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Here is a sketch showing the triangle:
I assume what is meant by "Label the midpoints of each side P, Q, and R respectively"
is for P to be the midpoint of AB,
Q to be the midpoint of BC,
and R to be the midpoint of AC,
so the triangle with labeled midpoints would be
The coordinates of each midpoint area averages of the coordinates of the vertices at the end of the side.
For side AB, the midpoint is P%28%286%2B10%29%2F2%2C%282%2B4%29%2F2%29=P%288%2C3%29 .
For side BC, the midpoint is Q%28%2810-2%29%2F2%2C%284%2B8%29%2F2%29=Q%284%2C6%29 .
For side AC, the midpoint is R%28%286-2%29%2F2%2C%282%2B8%29%2F2%29=R%282%2C5%29 .
Then, we can draw the segments connecting each vertex to the midpoint of the opposite side. Those segments are the medians of the triangle, and all 3 intersect at one point, the centroid of the triangle.
We can represent the lines formed by extending those segments by equations and find the intersection point.
We can also calculate the coordinates of the centroid as
x%28centroid%29=%28x%5BA%5D%2Bx%5BB%5D%2Bx%5BC%5D%29%2F3 and y%28centroid%29=%28y%5BA%5D%2By%5BB%5D%2By%5BC%5D%29%2F3 .
Using those formulas,
x%28centroid%29=%286%2B10%2B%28-2%29%29%2F3=14%2F3 and y%28centroid%29=%282%2B4%2B8%29%2F3=14%2F3 .
So the centroid is point 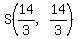S%2814%2F3%2C14%2F3%29 .
If you are expected to write the equations of the lines that contain the medians,
you only need two of the three lines (any two).
For example:
For line AQ, the slope is %282-6%29%2F%286-4%29=-4%2F2=-2 .
The line passing through 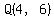Q%284%2C6%29 with slope -2 has the equations
y-6=-2%28x-4%29<--->y-6=-2x%2B8%29<--->y=-2x%2B8%2B6%29<--->y=-2x%2B14%29 .
For line CP, the slope is %283-8%29%2F%288%2B2%29=-5%2F10=-1%2F2 .
The line passing through 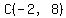C%28-2%2C8%29 with slope -1%2F2 has the equations
y-8=%28-1%2F2%29%28x%2B2%29<--->y-8=%28-1%2F2%29x-1<--->y=%28-1%2F2%29x-1%2B8<--->y=-%281%2F2%29x%2B7 .
The coordinates for the intersection of lines AQ and CP are given by
system%28y=-2x%2B14%2Cy=-%281%2F2%29x%2B7%29 --> system%28y=-2x%2B14%2C-2x%2B14=-%281%2F2%29x%2B7%29 --> system%28y=-2x%2B14%2C-2x%2B%281%2F2%29x=7-14%29 --> system%28y=-2x%2B14%2C%28-3%2F2%29x=-7%29 --> system%28y=-2x%2B14%2Cx=%28-7%29%28-2%2F3%29%29 --> system%28y=-2x%2B14%2Cx=14%2F3%29 --> system%28y=-2%2814%2F3%29%2B14%2Cx=14%2F3%29 --> system%28y=-28%2F3%2B42%2F3%2Cx=14%2F3%29 --> system%28y=14%2F3%2Cx=14%2F3%29
For line BR, the slope is %284-5%29%2F%2810-2%29=-1%2F8 .
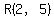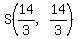We could calculate the equation of the line passing through R%282%2C5%29 with slope -1%2F8 , and verify that it passes through S%2814%2F3%2C14%2F3%29 ,
but it should because we know that all 3 medians intersect at the same point.