Question 93150This question is from textbook
: Problem:
One leg of a right triangle has a length of 3m. The other sides have lengths that are consecutive integers. Find these lenths.
The other leg is ____ m
The length of the hypotenuses is ____m
I get the consecutive inegers n, n+1
and if I use the formula a^2 + b^2 = c^2 - I don't know what
to plug in for c. I've been shown several ways, and now
I'm just confused.
Thanks!!!
This question is from textbook
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! Well, on this problem you do have to make at least one assumption:
The given side of 3 meters is (or is not) the hypotenuse.
If you assume that it is the hypotenuse, it is therefore the longest of the three sides of the right triangle.
Since the other two sides are consective integers and each is less then 3, they can only be 1 and 2 mters in length.
Well, as soon as you apply the Pythagorean theorem, you soon see that this cannot be so, because  does not equal  .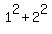
So the 3-meter side is one of the legs, right?
Now you have a choice: Is it the shorter leg or the longer leg (not the hypotenuse)?
Let's try the shorter leg.
So the hypotenuse, being the longest side must be n+1 and the other leg must be n. Applying the Pythagorean theorem: 
 Subtract  from both sides.
 and...
So, the hypotenuse is 5 meters,and the other leg is 4 meters.
If you were familiar with Pythagorean triplets, you could easily have guessed this result.
|
|
|
