Question 911743: Find the area in  , of a right triangle that has one acute angle to twice the other, and has a hypotenuse equal to 5 cm.
A) 6
B) 
C) 
D) 12
E)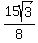 
Found 2 solutions by ichigo449, josmiceli:
Answer by ichigo449(30)   (Show Source):
You can put this solution on YOUR website! Let x be one of the acute angles. Then, as we have a right triangle, we obtain the equation: 3x+90=180, or x = 30 so 2x = 60, and we have a 30-60-90 triangle. Now, we have many ways to proceed to find an answer and I suggest you try to find 3 separate ways to get the area from this step. I will give you one as follows: Let H be the hypotenuse of the triangle, then for a 30-60-90 triangle the shortest side is H/2, and the middle length side is 1/2(H*sqrt(3)). Knowing these facts we can express the area as: H^2*sqrt(3)/8 by the regular area = 1/2(base*height) with base = H/2 and height = 1/2(H*sqrt(3)). We therefore conclude, by plugging in H = 5 that the answer is B. Have a nice day and good luck with your class.
Answer by josmiceli(19441)  (Show Source):
|
|
|
