SOLUTION: Find two integers whose product is 296 such that one of the integers is three less than five times the other integer. I've tried working this out and can't figure it out! Someone

Algebra ->  Triangles -> SOLUTION: Find two integers whose product is 296 such that one of the integers is three less than five times the other integer. I've tried working this out and can't figure it out! Someone       Log On


   

Question 715404: Find two integers whose product is 296 such that one of the integers is three less than five times the other integer.
I've tried working this out and can't figure it out! Someone please help.
-Kassidy
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
Use the words to make equations that relate the two numbers.


The first equation is "Find two integers whose product is 296 ". Product is the result of multiplication. Call the integers x and y. x*y=296.


The second equation is " one of the integers is three less than five times the other integer. x = 5*y-3 (is means =, three less than means subtract three, and five times means 5*.)


Substitute the value the second equation gives for x (that's (5y-3)) into the first equation. Then solve it for y. xy=296 becomes (5y-3)*y = 296.


Distribute the y: 5y^2 -3y = 296 Subtract 296 from both sides 5y^2 -3y-296=0.


Find y using the quadratic equation 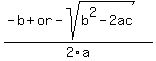%28-b+%2B+or+-+sqrt%28b%5E2+-+2ac%29%29%2F2a where a, b and c are from the equation ax^2 +bx +c. In this problem a = 5, b=-3 and c=-296.


%283+%2B+or+-+sqrt%285929%29%29%2F10+=+%283+%2B+or+-+77%29%2F10 = 80/10 or -74/10 = 8 or -7.4


The problem states that both numbers are integers. So discard y=-7.4. That leaves y=8. If y = 8 you can find x: x*8=296 ---> x=296/8 = 37.

Hope the solution helped. Sometimes you need more than a solution. Contact fcabanski@hotmail.com for online, private tutoring, or personalized problem solving (quick for groups of problems.)