Question 674343: how do I find the area of an iscoseles triangle when I've only been given the measurements of two sides using the sine rule: 1/2(ab)sinC
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the formula you are using is area of a triangle is equal to 1/2 * base * height.
the base is a
the height is b * sin(c)
my diagram of your triangle is shown below:
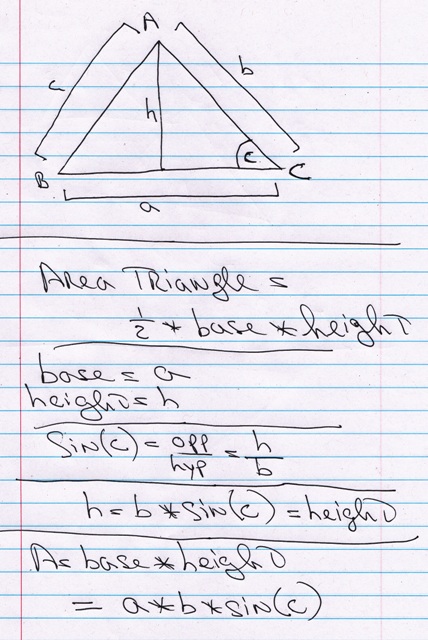
in the diagram, h is the height and a is the base.
using trigonometry, we get:
sin(c) = oppositve / hypotenuse = h / b
multiplying both sides of this equation by b, we get:
h = b * sin(c)
since they're equal, we can substitute one for the other.
the formula is area = 1/2 * base * height.
the base is equal to a.
the height is equal to b * sin(c)
the formula becomes:
area = 1/2 * a * b * sin(c)
to find the area of the triangle using this formula, you need to know what angle C is.
Answer by ikleyn(53429)  (Show Source):
You can put this solution on YOUR website! .
how do I find the area of an  isosceles triangle when I've only been given
the measurements of two sides using the sine rule: 1/2(ab)sinC.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First, the formula works for any triangle, not necessary isosceles.
Second, you ask " How do I find . . . " - the answer is: simply substitute the given/known values into the formula,
exactly as using any other formula. By the way, in addition to the sides 'a' and 'b',
the measure of the angle 'C' between these side is assumed to be given, or known, or derived from other data in the problem.
If nothing more than the sides 'a' and 'b' is given, you will not be able to find the area of this triangle.
Then your formula and the problem itself " has no enough fuel " to deliver you to your destination.
Third, the " sine rule " is irrelevant to this formula.
Summarizing, I would say that this request is formulated in a confused manner,
its purpose is hidden in the fog and is not clearly visible.
|
|
|
