SOLUTION: Hi, I had this problem for homework and I couldn't get it. THANKS FOR HELPING!! <a href="http://photobucket.com/" target="_blank"><img src="http://i73.photobucket.com/albums/i22

Click here to see ALL problems on Triangles

Question 65834: Hi, I had this problem for homework and I couldn't get it. THANKS FOR HELPING!!

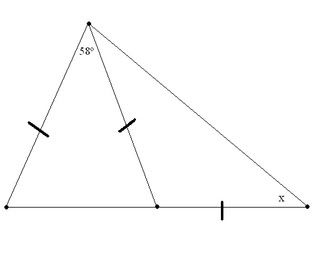
Find X.

Found 3 solutions by Earlsdon, Cintchr, stanbon:
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website!
Using the well-known fact that in any plane triangle the sum of the three angles is 180 degrees. Let's find the two base angles of the isosceles triangle on the left side of your diagram.
In any isosceles triangle, the two base angles are equal, and the sum of the three angles (the two base angles and the vertex angle) in this triangle is 180 degrees. Let y = the measure of one of the base angles, then we can write:
58 + y + y = 180 Simplifying this, we get:
58 + 2y = 180 Subtracting 58 from both sides, we get:
2y = 122 Finally, dividing by 2, we have:
y = 61 degrees.
Now that we know the measure of two base angles of the isosceles triangle, we can find the the measure of the other base angle of the isosceles triangle on the right. Let's call that one angle z.
We know that angle y and angle z are supplementary angles and their sum is 180 degrees.
This allows us to find angle z as follows:
y + z = 180 But angle y = 61 degrees, so substitute this for y:
61 + z = 180 Subtract 61 from both sides.
z = 119 degrees.
Using the fact that in an isosceles triangle, the base angles are equal, we know that one of the base angles is x degrees so the other one must x degrees also. Again, we know that the sum of the angles in a plane triangle is 180 degrees. So, we can write:
61 + x + x = 180 Subtracting 61 from both sides, we get:
2x = 119 Dividing by 2 we find that:
x = 59.5 degrees.

Answer by Cintchr(481)   (Show Source):
You can put this solution on YOUR website!
Alright ... the Triangle on the left is Isocoles. The two base angles (we will label them 'y' ) are equal. So if the top angle is 58 deg, then the bottom two are each equal 61 deg.

In the triangle on the right ... the angle that is next to the 61 deg angle is 119 deg, because it is the supplement to the other angle, and they make a linear pair. (label this one 'z' )

Still looking at the Triangle on the right, the angle measuring 119 is the vertex of yet another isocoles triangle which means the other two are congruent.

Here is your check:

This is the LARGE triangle.

YES!!!

Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website!
It would help to label the vertices of the outer triangle.
Start on the left side and go clockwise to mark angles A,B,C.
C is at the top.
There are two isosceles triangles: one on the left, one on the right.
The left has an apex angle of 58.
Each base angle in the left isosceles triangle is (1/2)(180-58)=61 degrees.
The point situated between C and A has two angles at it: one is a 61 degree
base angle; the other is the supplement of 61 which is 180-61=119 degrees.
Then each of the base angles of the RIGHT isosceles triangle is (1/2)(180-119)
=30.5 degrees
One of those base angles is x.
So x=30.5 degrees
Cheers,
Stan H.