Question 622387: In a right angled triangle AB is hypotenuse.D,E and F are the mid-points of BC,AB and AC respectively.P,Q and R are the min-points of AD,CE and BF respectively.so prove that
((PA)^2 +(PB)^2 +(PC)^2)+((QA)^2 +(QB)^2 +(QC)^2)+((RA)^2 +(RB)^2 +(RC)^2)=(AB)^2
Answer by Edwin McCravy(20061)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If that's a true equation, the best way to prove it is with coordinate
geometry.
 But the sum of all those squares will obviously be greater than
just AB², but I'll try to prove it anyway, and see what happens.
Suppose A has the coordinates A(4a,0) and B has coordinates B(0,4b).
[I chose 4a and 4b instead of a and b to avoid fractions with the midpoint formula)
Then we use the midpoint formula,
Midpoint =
But the sum of all those squares will obviously be greater than
just AB², but I'll try to prove it anyway, and see what happens.
Suppose A has the coordinates A(4a,0) and B has coordinates B(0,4b).
[I chose 4a and 4b instead of a and b to avoid fractions with the midpoint formula)
Then we use the midpoint formula,
Midpoint = 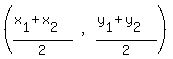 to find all these coordinates:
A(4a,0)
B(0,4b)
C(0,0)
D(0,2b)
E(2a,2b)
F(2a,0)
P(2a,b)
Q(a,b)
R(a,2b)
Then we use the distance formula, which is
d =
to find all these coordinates:
A(4a,0)
B(0,4b)
C(0,0)
D(0,2b)
E(2a,2b)
F(2a,0)
P(2a,b)
Q(a,b)
R(a,2b)
Then we use the distance formula, which is
d = 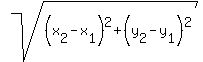 ,
with both sides squared:
d² = (x2 - x1)² + (y2 - y1)²
to find
PA² = (4a-2a)²+(0-b)² = (2a)²+(-b)² = 4a²+ b²
PB² = (0-2a)²+(4b-b)² = (-2a)²+(3b)² = 4a²+9b²
PC² = (0-2a)²+(0-b)² = (-2a)²+(-b)² = 4a²+ b²
QA² = (4a-a)²+(0-b)² = (3a)²+(-b)² = 9a²+ b²
QB² = (0-a)²+(4b-b)² = (-a)²+(3b)² = a²+9b²
QC² = (0-a)²+(0-b)² = (-a)²+(-b)² = a²+ b²
RA² = (4a-a)²+(0-2b)² = (3a)²+(-2b)² = 9a²+4b²
RB² = (0-a)²+(4b-2b)² = (-a)²+(2b)² = a²+4b²
RC² = (0-a)²+(0-2b)² = (-a)²+(-2b)² = a²+4b²
-----------------------------------------------
PA²+PB²+PC²+QA²+QB²+QC²+RA²+RB²+RC² =34a²+34b²
But
AB² = (0-4a)²+(4b-0)² = (-4a)²+(4b)² = 16a²+16b²
So the equation you were asked to prove is not true.
What is true is
PA²+PB²+PC²+QA²+QB²+QC²+RA²+RB²+RC² = ,
with both sides squared:
d² = (x2 - x1)² + (y2 - y1)²
to find
PA² = (4a-2a)²+(0-b)² = (2a)²+(-b)² = 4a²+ b²
PB² = (0-2a)²+(4b-b)² = (-2a)²+(3b)² = 4a²+9b²
PC² = (0-2a)²+(0-b)² = (-2a)²+(-b)² = 4a²+ b²
QA² = (4a-a)²+(0-b)² = (3a)²+(-b)² = 9a²+ b²
QB² = (0-a)²+(4b-b)² = (-a)²+(3b)² = a²+9b²
QC² = (0-a)²+(0-b)² = (-a)²+(-b)² = a²+ b²
RA² = (4a-a)²+(0-2b)² = (3a)²+(-2b)² = 9a²+4b²
RB² = (0-a)²+(4b-2b)² = (-a)²+(2b)² = a²+4b²
RC² = (0-a)²+(0-2b)² = (-a)²+(-2b)² = a²+4b²
-----------------------------------------------
PA²+PB²+PC²+QA²+QB²+QC²+RA²+RB²+RC² =34a²+34b²
But
AB² = (0-4a)²+(4b-0)² = (-4a)²+(4b)² = 16a²+16b²
So the equation you were asked to prove is not true.
What is true is
PA²+PB²+PC²+QA²+QB²+QC²+RA²+RB²+RC² = 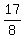 AB²
Sorry, but what you were asked to prove just isn't true.
Were some of those plus signs supposed to be minus signs?
Edwin AB²
Sorry, but what you were asked to prove just isn't true.
Were some of those plus signs supposed to be minus signs?
Edwin
|
|
|