SOLUTION: The measures of the angles of a quadrilateral are in the ratio 2:4:5:7. Find the measures.

Algebra ->  Triangles -> SOLUTION: The measures of the angles of a quadrilateral are in the ratio 2:4:5:7. Find the measures.      Log On


   

Question 536464: The measures of the angles of a quadrilateral are in the ratio 2:4:5:7. Find the measures.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The measures of the angles of a quadrilateral are in the ratio 2:4:5:7.
Find the measures.
The four interior angles of an n-side polygon is given by the formula

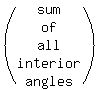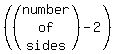%28matrix%285%2C1%2Csum%2C+of%2C+all%2C+interior%2C+angles%29%29 = %28%28matrix%283%2C1%2Cnumber%2C+of%2C+sides%29%29-2%29×180°

A quadrilateral has 4 sides so,

%28matrix%285%2C1%2Csum%2C+of%2C+all%2C+interior%2C+angles%29%29 = (4-2)×180° = 2×180° = 360°

If we wish to divide a number N into 4 parts in the ratio of a:b:c:d, the
parts are given by these formulas:

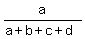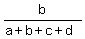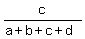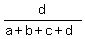a%2F%28a%2Bb%2Bc%2Bd%29×N, b%2F%28a%2Bb%2Bc%2Bd%29×N, c%2F%28a%2Bb%2Bc%2Bd%29×N, and d%2F%28a%2Bb%2Bc%2Bd%29×N

So since we wish to divide 360° into 4 parts in the ratio of 2:4:5:7 


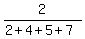2%2F%282%2B4%2B5%2B7%29×360° = 2%2F18×360° = 1%2F9×360° = %22360%B0%22%2F9 = 40°

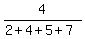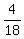4%2F%282%2B4%2B5%2B7%29×360° = 4%2F18×360° = 2%2F9×360° = %22720%B0%22%2F9 = 80°

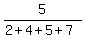5%2F%282%2B4%2B5%2B7%29×360° = 5%2F18×360° = %221800%B0%22%2F100 = 100°

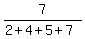7%2F%282%2B4%2B5%2B7%29×360° = 7%2F18×360° = %222520%B0%22%2F18 = 140°

We can check by adding the 4 angles to see if we get 360°

                  40° + 80° + 100° + 140° = 360°

We get 360°, so we must not have made any mistakes.

Edwin