Question 515233: Can a triangle exist having sides of 11, 12 and 13 in length, and how do you prove it? We know it's not a right triangle or an equilateral or isosceles, so how do you know for other triangles?
Found 2 solutions by drcole, josmiceli:
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! In general, a triangle on the plane exists with sides of length a, b, and c as long as the length of any one side is strictly less than the sum of the lengths of the other two sides:
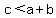 and and  and and 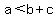
This phenomenon is called the Triangle Inequality. So a triangle with sides 11, 12, and 13 should exist, since 11 < 12 + 13 = 25, 12 < 13 + 11 = 24, and 13 < 11 + 12 = 23. That isn't very satisfying, though, since it doesn't actually give us a triangle. So let's actually construct a triangle with sides 11, 12, and 13. You can do this algebraically, but try it using a compass and a ruler: take a sheet of paper and make a point A. Then use a ruler to make a second point B 13 centimeters away from the first (the direction doesn't matter). Next, set your compass so that the two tips are 11 centimeters apart, and draw a circle centered at point A. Once you make this circle, adjust your compass so that the two tips are 12 centimeters apart, and draw a circle centered at point B. The two circles you drew should intersect at two points. Pick one of these points and call it C. Now use your ruler to draw the line segments AB, BC, and CA. The line segment AB has length 13 centimeters, the line segment AC has length 11 centimeters, and the line segment BC has length 12 centimeters. So you have constructed a triangle with sides of length 11, 12, and 13, which proves that such a triangle exists.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you lay one of the sides on a table,
say the 13 side. then the sum of the other 2 sides
is greater than 13 ( 11 + 12 = 23 ), and
that means they have to meet somewhere
|
|
|