Question 491334: Two sides of a triangle are sqrt(3) and sqrt(2) units.The medians to these sides are perpendicular to each other.Find the length of the third side.
Answer by cleomenius(959)   (Show Source): (Show Source):
You can put this solution on YOUR website! This was a tough problem, basically I found a similiar one on the web, so the solution is pretty much their's, I was kind of of torn about using it but I didn't want it to get hung up, and I like both sites so I'm passing it on.
http://www.qbyte.org/puzzles/p100s.html
My suggestion is follow along with his diagram.
In the diagram below, angleBCA = angleA'CB', and CA'/CB = CB'/CA = ½.
Hence triangles CAB and CB'A' are similar; and A'B' = ½BA.
Let AA' and BB' intersect at D.
Let A'D = x, B'D = y, AD = z, BD = w. Let AB = c, so that A'B' = ½c.
Triangle ABC, with perpendicular medians AA' and BB', intersecting at D, and line segment A'B'. Length AB=c, A'B'=c/2, A'D=x, B'D=y, AD=z, BD=w.
Applying Pythagoras' Theorem to each of the four right-angled triangles shown in the diagram:
triangleA'B'D implies y2 + x2 = c2/4. (1)
triangleB'AD implies y2 + z2 = 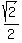 ^2 = 1/2. (2) ^2 = 1/2. (2)
triangleABD implies w2 + z2 = c2. (3)
triangleBA'D implies w2 + x2 = 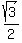 ^2 = 3/4. (4) ^2 = 3/4. (4)
Then (1) − (2) + (3) − (4) implies 0 = 5c^2/4 − 5/4.
Hence c^2 = 1.
Therefore the length of side AB is 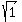 . .
Cleomenius.
|
|
|