Question 476956: I'm trying to figure out how to find the perimeter to an isosceles triangle where I am only given one side which is 14, and the only other information is that the other two sides are congruent.
Found 2 solutions by Theo, richard1234:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! you are given the length of the base of the isosceles triangle.
with only this information, you can construct a limitless number of isosceles triangles.
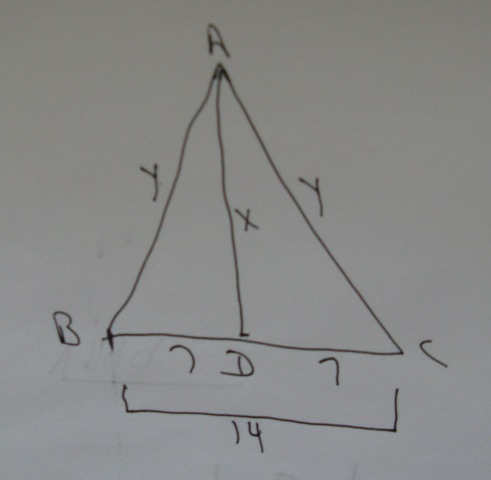
check out the attached picture to see what I mean.
BC is the base.
AB and AC are the congruent sides.
AD is a perpendicular dropped from angle A intersecting with the base at D.
since this is an isosceles triangle, AD splits the base into 2 equal parts.
Those are BD and CD which are each equal to 7.
let y equal the length of AB and the length of AC
leg x equal the length of AD.
Since AD is perpendicular to the base, it forms 90 degree angles with the base.
Angles ADB and ADC are each 90 degrees.
This forms 2 right triangles.
They are triangle ADB and triangle ADC.
Since this is an isosceles triangle, angles B and C are equal to each other (they are congruent).
we can use the pythagorean formula to find the length of AD and the length of AC, but only in terms of each other since we don't have enough information to narrow the problem down to a specific result.
the pythagorean formula is:
hypotenuse squared = first leg squared plus second leg squared.
we'll call AD the first leg of right triangle ADC
we'll call DC the second leg of right triangle ADC
we'll call AC the hypotenuse of right triangle ADC
the length of AD is equal to x
the length of DC is equal to 7
the length of AC is equal to y
our formula becomes:
x^2 + 7^2 = y^2
this becomes:
x^2 + 49 = y^2
if we want to solve for the height of the triangle, this formula becomes:
x^2 = y^2 - 49
if we want to solve for the side of the triangle, this formula becomes:
y^2 = x^2 + 49 (it is left as is).
in order to find y, we need to know x.
in order to find x, we need to know y.
we'll assume we want to find y which is the congruent leg of the isosceles triangle.
the formula is:
y^2 = x^2 + 49 which becomes:
y = sqrt(x^2 + 49)
the perimeter of our isosceles triangle will be equal to:
p = 2y + 14 (p stands for perimeter.)
but...
we need to know x in order to find y.
since we can find any number of values for x, this means that our isosceles triangle will have any number of values for y which means that our isosceles triangle will have any number of values for p.
here's a table that lists a few values of y and p based on specified values of x.
DC AD AC perimeter
7 1 7.071067812 21.14213562
7 2 7.280109889 21.56021978
7 3 7.615773106 22.23154621
7 4 8.062257748 23.1245155
7 5 8.602325267 24.20465053
7 6 9.219544457 25.43908891
7 7 9.899494937 26.79898987
7 8 10.63014581 28.26029163
7 9 11.40175425 29.8035085
7 10 12.20655562 31.41311123
7 11 13.03840481 33.07680962
7 12 13.89244399 34.78488798
7 13 14.76482306 36.52964612
7 14 15.65247584 38.30495168
the length of DC is always 7.
the length of AD is equal to x in the diagram, but is equal to the specified values under the heading of AD in this table.
the length of AC is equal to y in the diagram, but is equal to the result of the equation y = sqrt(49+x^2) in this table.
the perimeter is equal to 2 times the length of AC plus the length of BC which is always equal to 14 because that's what was given.
you can see that you can have an infinite number of isosceles triangle which will create an infinite number of perimeters if the only information you have is that the base of the isosceles triangle is equal to 14.
your answer is:
without any other information other than the length of the base of the isosceles triangle, an infinite number of isosceles triangles can be drawn with a different altitude and a different length for the other 2 sides of the triangle.
in order to find the perimeter of one of the triangle, you have to be provided with either:
the height of the triangle.
the length of the congruent legs of the triangle.
the measure of the angle that is opposite the base of the triangle.
the measure of the congruent angles of the triangle.
-----
each of these would be in addition to the length of the base.
-----
note:
in an isosceles triangle:
the angles formed by the intersection of the legs of the triangle and the baswe of the triangle are congruent.
that would be angles B and C in the diagram.
the sides opposite these angles are congruent.
that would be sides AB and AC in the diagram.
here's your diagram
Answer by richard1234(7193)  (Show Source):
You can put this solution on YOUR website! If the other sides have length "x", then the perimeter is 14 + x + x = 14+2x. Note that x must be greater than 7 due to the triangle inequality, so 14+2x > 28. This is all that we know about the perimeter.
|
|
|
