Question 475217: What is the area of an isosceles triangle with sides of 7, 7, and 12?
Found 2 solutions by jim_thompson5910, richard1234:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! For more help, check out this solver.
| Solved by pluggable solver: Hero's (or Heron's) Formula (Used to Find the Area of a Triangle Given its Three Sides) |
In order to find the area of a triangle 'A' with side lengths of 'a', 'b', and 'c', we can use Hero's Formula:
 where S is the semiperimeter and it is defined by where S is the semiperimeter and it is defined by 
Note: "semi" means half. So the semiperimeter is half the perimeter.
So let's first calculate the semiperimeter S:
 Start with the semiperimeter formula. Start with the semiperimeter formula.
 Plug in Plug in  , ,  , and , and  . .
 Add. Add.
 Divide. Divide.
----------------------------------------
 Now move onto Hero's Formula. Now move onto Hero's Formula.
 Plug in Plug in  , ,  , ,  , and , and  . .
 Subtract. Subtract.
 Multiply. Multiply.
 Take the square root of Take the square root of 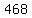 to get to get 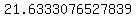 . .
So the area of the triangle with side lengths of  , ,  , and , and  is roughly is roughly 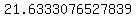 square units. square units.
|
For more help, check out this solver.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! You can use Heron's formula. Or, given that the triangle is isosceles you can draw an altitude from the vertex to the base (of length 12) so that you have two right triangles with legs h and 6, and hypotenuse 7. Here it should be pretty easy.
|
|
|