Question 434161: A(0,5)B(7,1)C(-3,-2) triangle. How would i find the area?
Found 2 solutions by richard1234, Alan3354:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! The area is equal to 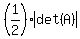 , where , where 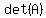 is the determinant of the 3x3 matrix formed by using the vertices with a set of 1's. The matrix we are evaluating is equal to is the determinant of the 3x3 matrix formed by using the vertices with a set of 1's. The matrix we are evaluating is equal to
0 5 1
7 1 1
-3 -2 1
I'll leave the arithmetic to you.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A(0,5)B(7,1)C(-3,-2) triangle. How would i find the area?
------------
There are several ways to do this.
You can find the lengths on the 3 sides, then use Heron's Law.
Or, with the 3 sides you can find one of the altitudes, then use Area = b*h/2
Or, find one of the angles after finding the 3 sides and use Area = the product of 2 sides x the sine of the included angle.
-----------
I like this method, tho.
Make a matrix, repeating the first point
A B C A
0 7 -3 0
5 1 -2 5
----------
Add the daigonal products starting at the upper left
0*1 + 7*-2 + -3*5 = -29
Do the same from the lower left
5*7 + 1*-3 + -2*0 = 32
The difference is 61
The area is 61/2 = 30.5 sq units
----------------------
This works for any polygon, with any number of sides.
It doesn't seem to be well known.
|
|
|