Question 389248: If the vertices of an equilateral triangle are (0,4), (0,0), and (2square root3, 2), how many of these triangles are possible?
Found 2 solutions by richard1234, ewatrrr:
Answer by richard1234(7193)   (Show Source):
Answer by ewatrrr(24785)  (Show Source):
You can put this solution on YOUR website!
Hi,
vertices of an equilateral triangle:
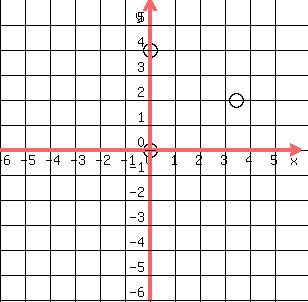
(0,4), (0,0), and (2square root3, 2) OR Pt(3.464,2) Note:{{sqrt(3) = 1.732}}}
how many of these triangles are possible: ONE
|
|
|
