SOLUTION: Two vertices of a triangle are (0,6) and (4,0), and the medians intersect at (0,2). Find the third vertex of the triangle.

Algebra ->  Triangles -> SOLUTION: Two vertices of a triangle are (0,6) and (4,0), and the medians intersect at (0,2). Find the third vertex of the triangle.      Log On


   

Question 345491: Two vertices of a triangle are (0,6) and (4,0), and the medians intersect at (0,2). Find the third vertex of the triangle.
Found 2 solutions by Fombitz, ewatrrr:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
A:(0,6)
B:(4,0)
C:(x,y)
Assume that the final vertex is located at(x,y).
Then the median connecting (x,y) to the midpoint of AB, located at (2,3), has a slope,since it also goes through (0,2), of,
m=%283-2%29%2F%282-0%29=1%2F2
and a y-intercept of 2.
1.y=%281%2F2%29x%2B2
.
.
.
The median connecting (4,0),(0,2), and the midpoint of AC has a slope of,
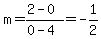
m=%282-0%29%2F%280-4%29=-1%2F2
and a y-intercept of 2.
y=-%281%2F2%29x%2B2
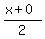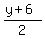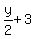The midpoint of AC is (%28x%2B0%29%2F2,%28y%2B6%29%2F2) or (x%2F2,y%2F2%2B3).
It also satisfies the line,
y=-%281%2F2%29x%2B2
y%2F2%2B3=-%281%2F2%29%28x%2F2%29%2B2
2y%2B12=-x%2B8
2.x%2B2y=-4
.
.
.
From eq. 1,
2y=x%2B4
Substituting into eq. 2,
x%2Bx%2B4=-4
2x=-8
highlight%28x=-4%29
Then
2y=-4%2B4
2y=0
highlight%28y=0%29
The final vertex is located at (-4,0)

Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
Hi,
Recommend Sketching out the points given first:

The question states medians intersect at pt(0,2)
*Note: Medians go from a vertex to the midpoint of the opposing side
.
Sketch determines the midpoint of the opposing side of vertex (0,6) would be (0,0)
.
the third vextex would be (-4,0)