SOLUTION: I have an equilateral triangle with an area of 30 square centimeters. I need to find the base and height of the triangle.

Algebra ->  Triangles -> SOLUTION: I have an equilateral triangle with an area of 30 square centimeters. I need to find the base and height of the triangle.       Log On


   

Question 17499: I have an equilateral triangle with an area of 30 square centimeters. I need to find the base and height of the triangle.
Found 2 solutions by xcentaur, cleomenius:
Answer by xcentaur(357) About Me  (Show Source):
You can put this solution on YOUR website!
For an equilateral triangle,
Area is given by
+A=+%28s%5E2%29sqrt%283%29%2F4+
where s is the length of the side


+30+=+s%5E2%2Asqrt%283%29%2F4+
+30%2A4%2Fsqrt%283%29+=+s%5E2+
+3%2A40%2Fsqrt%283%29+=+s%5E2+
+sqrt%283%29%2A40+=+s%5E2+
+s=+sqrt%2840%2Asqrt%283%29%29+
+s=+sqrt%28sqrt%2840%2A40%2A3%29%29+
+s=+sqrt%28sqrt%284800%29%29+
Clear till here? Good.
Now we have to take factors twice.
So we get
+sqrt%284800%29=40%2Asqrt%283%29+ ........[first time]
+sqrt%2840%2Asqrt%283%29%29=2%2Asqrt%285%29%2Asqrt%282%29%2Asqrt%283%29......[second time]
+sqrt%2840%2Asqrt%283%29%29=2%2Asqrt%2810%2Asqrt%283%29%29......[simplified]
Therefore we get our value of 's' as 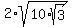2%2Asqrt%2810%2Asqrt%283%29%29


+A=+%28s%5E2%29sqrt%283%29%2F4+=+%281%2F2%29bh+
Now base and side are equal,therefore
+%28s%5E2%29sqrt%283%29%2F4+=+%281%2F2%29bh+
+%28s%5E2%29sqrt%283%29%2F4+=+%281%2F2%29sh+
+s%2Asqrt%283%29%2F4+=+%281%2F2%29h+
+s%2Asqrt%283%29%2F2+=+h+
+h+=+%28sqrt%283%29%2F2%29%2A2%2Asqrt%2810%2Asqrt%283%29%29
+h+=+sqrt%283%29%2Asqrt%2810%2Asqrt%283%29%29+
+h=+sqrt%283%2A10%2Asqrt%283%29%29+
+h=+sqrt%2830%2Asqrt%283%29%29+


So we have our values as
+s+=+2%2Asqrt%2810%2Asqrt%283%29%29+
+h+=+sqrt%2830%2Asqrt%283%29%29+


We can verify this using the [A=1/2bh] formula,
Area=1/2*s*h
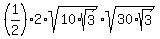
+%281%2F2%29%2A2%2Asqrt%2810%2Asqrt%283%29%29%2Asqrt%2830%2Asqrt%283%29%29+
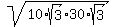
+sqrt%2810%2Asqrt%283%29%2A30%2Asqrt%283%29%29+
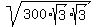
+sqrt%28300%2Asqrt%283%29%2Asqrt%283%29%29+
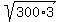
+sqrt%28300%2A3%29+
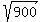
+sqrt%28900%29+
+30+


And thus we know that our values for s and h are correct.
Hope this helps,
Prabhat


Answer by cleomenius(959) About Me  (Show Source):
You can put this solution on YOUR website!
We can use the formula for Area of an equilateral triangle to find the side length.
Area = s^2sqrt%283%29/4
30 = s^2sqrt%283%29/4
120 = s^2sqrt%283%29
69.28 = s^2
8.23 cm = s
the altitude h of an equilateral triangle is :
h = side * sin 60 degrees.
8.23 (0.866) = 7.13 cm
To check,
1/2(8.23 * 7.13) = 29.3 Approx 30.