SOLUTION: Equilateral triangle ABC has sides of 14 cm. A circle of radius 2 cm inside it is tangent to sides AB & AC. Find the distance from the circle's centre to side BC, in cm.

The center of the circle lies on the bisector of angle A.


So, if you draw perpendicular line from the center to the side AB,
you will get right angled triangle with one leg of 2 cm (as the radius of the circle).


This right angled triangle is (30,60,90)-degrees; therefore the distance from the center 
of the circle to vertex A, as the hypotenuse in this triangle, is twice the radius, or 4 cm.


Next, the altitude of the equilateral triangle ABC is   =  = .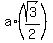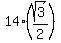


From it, you deduce that the distance from the center of the circle to the side BC is

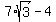     = 8.124355653... centimeters.


It is the  ANSWER,  and you can round the number appropriately.