Question 1208906: The area of a triangle is divided into 3 equal parts by line segments parallel to one side. If the length of that side is 18 cm, find the length of the longest line segment inside the triangle, in cm.
Answer by ikleyn(52747)   (Show Source):
You can put this solution on YOUR website! .
The area of a triangle is divided into 3 equal parts by line segments parallel to one side.
If the length of that side is 18 cm, find the length of the longest line segment inside
the triangle, in cm.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let the triangle be ABC, and the segment of interest be DE, parallel to the side BC.
Let x be the length of the segment DE.
Then triangles ABC and ADE are similar, and the similarity coefficient is  ,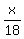
from lesser triangle ADE to greater triangle ABC.
The ratio of the area ADE to the area ABC is the square of of the similarity coefficient.
From the other side, this ratio is 2/3.
So, we can write this equation
 = 2/3
to find x.
From this equation,
x^2 =  =  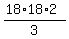= 6*18*2 = 216 square units.
Thus we find x =  =  = 14.6969 (rounded).
ANSWER. The longest line segment inside the triangle is , or about 14.6969 cm.
Solved.
|
|
|
