Question 1208855: The ratio of the complements of two angles is 3:2, and the ratio of their supplements is 9:8. Find the two original angles.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52878)   (Show Source):
You can put this solution on YOUR website! .
The ratio of the complements of two angles is 3:2, and the ratio of their supplements is 9:8.
Find the two original angles.
~~~~~~~~~~~~~~~~~~~~~~~
Let the angles be x and y degrees.
Then their complements are (90-x) and (90-y) degrees.
It gives us first equation
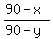 =  . (1)
From this equation
2*(90-x) = 3*(90-y),
180 - 2x = 270 - 3y
-2x + 3y = 90. (2)
Next, consider the supplementary angles (180-x) and (180-y) degrees.
For them, we have this equation
 =  . (3)
It gives
8*(180-x) = 9*(180-y),
1440 - 8x = 1620 - 9y
-8x + 9y = 180. (4)
Now we have the system of to equations
-2x + 3y = 90, (2)
-8x + 9y = 180. (4)
To solve, multiply equation (2) by 4; keep equation (4) as is
-8x + 12y = 360, (2')
-8x + 9y = 180. (4')
Now subtract equation (4') from equation (2'). You will get
3y = 180,
y = 60.
To find x, substitute y= 60 into equation (2)
-2x + 3*60 = 90 ---> 180 - 90 = 2x ---> 2x = 90 ---> x = 45.
ANSWER. The angles are 45 degrees and 60 degrees.
Solved.
Answer by greenestamps(13209)  (Show Source):
|
|
|
