 The green lines are the angle bisectors and we are to prove that the red lines
are parallel.
We will use two theorems which supposedly you have proved and can use:
Theorem 1:
The internal bisector of an angle of a triangle divides the opposite side
internally in the ratio of the corresponding sides containing the angle.
Theorem 2:
If a line divides two sides of a triangle proportionally (in the same ratio),
then it is parallel to the third side.
The internal bisector LE of angle TLN of triangle TLN divides the opposite side
MN internally in the ratio of the corresponding sides, LM and LN containing the
angle.
The green lines are the angle bisectors and we are to prove that the red lines
are parallel.
We will use two theorems which supposedly you have proved and can use:
Theorem 1:
The internal bisector of an angle of a triangle divides the opposite side
internally in the ratio of the corresponding sides containing the angle.
Theorem 2:
If a line divides two sides of a triangle proportionally (in the same ratio),
then it is parallel to the third side.
The internal bisector LE of angle TLN of triangle TLN divides the opposite side
MN internally in the ratio of the corresponding sides, LM and LN containing the
angle.


 The internal bisector LF of angle MLN of triangle MLN divides the opposite side
TN internally in the ratio of the corresponding sides, LN and MN containing the
angle.
The internal bisector LF of angle MLN of triangle MLN divides the opposite side
TN internally in the ratio of the corresponding sides, LN and MN containing the
angle.
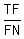

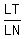 Since side LM is congruent to side LT, the right sides of the above equations are
equal, and therefore their left sides are equal also. (The ratios are equal).
Since side LM is congruent to side LT, the right sides of the above equations are
equal, and therefore their left sides are equal also. (The ratios are equal).


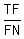 Line EF divides sides NM and NT of triangle MNT proportionally (in the same
ratio), so it is parallel to the third side MT.
Edwin
Line EF divides sides NM and NT of triangle MNT proportionally (in the same
ratio), so it is parallel to the third side MT.
Edwin