Question 1200779: 1. If one of the legs of a right triangle is three times the other and the perimeter of the triangle is 45m,find its area.
2. The area of a triangle is 65m^2 and the triangle is an equiangular triangle. Find the length of the three sides.
3. The area of a triangle is 8346m^2 and two of its interior angles are 37°25' and 56°17'. What is the length of the longest side?.
4. In a triangle ABC; AC= 60cm, BC= 30cm, and angle B=80°30',Find side AB.
Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Only giving help for #2.
Make a drawing and label all the parts with what you know or are given. The triangle is like two right triangles sharing the same long leg. Pythagorean Theorem Formula! Do the rest.
----
some help on #3
This maybe is not the neatest way to solve but if you draw the triangle using longest side
as horizontal segment, the smaller angle at left and the 56 deg 17 min angle at the right,
the other angle at top, and use interior angle sum rule, this angle at top is 88 degree 18 min.
The height, h or altitude cuts the horizontal base into lengths x, the left,
and p, the right.
You can make these three equations:
 . .
Three equations, three unknown variables.
Working along through that system, substituting for x and p, find

Use this to find value for 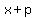 . .
Other neater way may be possible.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
|
|
|