Question 1199944: An airplane is flying east at a constant altitude of 28,000 meters. The pilot spots a ship at an angle of
depression of 18.5 degrees . After 73 seconds the angle of depression is 38.4 Degrees. Find the speed of the plane.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
An airplane is flying east at a constant altitude of 28,000 meters.
The pilot spots a ship at an angle of depression of 18.5 degrees.
After 73 seconds the angle of depression is 38.4 Degrees.
Find the speed of the plane.
~~~~~~~~~~~~~~~~~~~~~~~~~~
For the angle of 18.5°, tan(18.5°) =  ,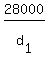
where  is the first horizontal diatance, measured at the sea level.
So, =  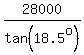=  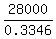= 83682 meters.
For the angle of 38.4°, tan(38.4°) =  ,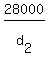
where  is the second horizontal diatance, measured at the sea level.
So, =  =  = 35327 meters.
Thus, in 73 seconds, the airplane covered 83682 - 35327 = 48355 meters.
Hence, the speed of the airplane is  = 662.397 m/s = 2384 km/h. ANSWER
Solved.
-----------------
To which direction the airplane is flying (east, west, north, south), it does not matter.
What does really matter in this problem, is that the pilot sees the ship straight ahead.
|
|
|
