Question 1199591: Im a triangle ABC.
Cos A/a = Cos B/b = Cos C/c, and a = 2. It is possible to compute the area of the
triangle, (Hint: compare the problem data with the Law of the Sines, compute ratios between the sines and cosines of the angles)
A) sqrt3/4
B) sqrt3/2
C) sqrt3
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I'm a triangle ABC.
Cos A/a = Cos B/b = Cos C/c, and a = 2. It is possible to compute the area of the
triangle, (Hint: compare the problem data with the Law of the Sines, compute ratios between the sines and cosines of the angles)
A) sqrt3/4
B) sqrt3/2
C) sqrt3
~~~~~~~~~~~~~~~~~~~
We are given Cos(A)/a = Cos(B)/b = Cos(C)/c. (1)
Let "p" be the common value of all these three ratios
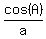 = = 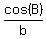 = = 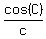 = p. (2)
Then
cos(A) = pa, (3)
cos(B) = pb, (4)
cos(C) = pc. (5)
From the other side, we have this "Law of Sines" formula = p. (2)
Then
cos(A) = pa, (3)
cos(B) = pb, (4)
cos(C) = pc. (5)
From the other side, we have this "Law of Sines" formula
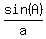 = = 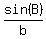 = =  . (6)
Let "q" be the common value of all these three ratios . (6)
Let "q" be the common value of all these three ratios
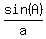 = = 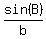 = =  = q. (7)
Then
sin(A) = qa, (8)
sin(B) = qb, (9)
sin(C) = qc. (10)
Divide (8) by (3); divide (9) by (4); divide (10) by (5). You will get then = q. (7)
Then
sin(A) = qa, (8)
sin(B) = qb, (9)
sin(C) = qc. (10)
Divide (8) by (3); divide (9) by (4); divide (10) by (5). You will get then
 = = 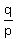 , ,
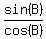 = = 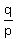 , ,
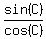 = = 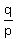 ,
or tan(A) = tan(B) = tan(C) = ,
or tan(A) = tan(B) = tan(C) = 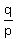 .
The tangents of three angles of a triangle are equal --- hence the angles are congruent A = B = C.
So, the triangle ABC is an equilateral triangle with the side length of 2 units.
Hence, its area is .
The tangents of three angles of a triangle are equal --- hence the angles are congruent A = B = C.
So, the triangle ABC is an equilateral triangle with the side length of 2 units.
Hence, its area is 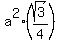 = =  = =  square units. square units.
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
cos(A)/a = cos(B)/b = cos(C)/c
cos(A)/a = cos(B)/b
cos(A)/cos(B) = a/b
Use the law of sines to apply similar steps:
sin(A)/a = sin(B)/b = sin(C)/c
sin(A)/a = sin(B)/b
sin(A)/sin(B) = a/b
We can see that:
cos(A)/cos(B) = a/b
cos(A)/cos(B) = sin(A)/sin(B)
which can be rearranged into
sin(B)/cos(B) = sin(A)/cos(A)
tan(B) = tan(A)
B = A
A = B
Follow a similar chain of logic to conclude that B = C.
We have A = B and B = C, so A = C
All three angles are the same measure.
A+B+C = 180
A+A+A = 180
3A = 180
A = 180/3
A = 60
Each angle is 60 degrees.
The triangle is equilateral.
Area of equilateral triangle with side length 's'
Area = 0.25*s^2*sqrt(3)
Area = 0.25*2^2*sqrt(3)
Area = sqrt(3)
Answer: C) sqrt(3)
|
|
|