SOLUTION: The lengths of the sides of a triangle are positive integers. One side has length 17 and the perimeter of the triangle is 54. If the area is also an integer, find the length of the

Algebra ->  Triangles -> SOLUTION: The lengths of the sides of a triangle are positive integers. One side has length 17 and the perimeter of the triangle is 54. If the area is also an integer, find the length of the      Log On


   

Question 1199461: The lengths of the sides of a triangle are positive integers. One side has length 17 and the perimeter of the triangle is 54. If the area is also an integer, find the length of the longest side.
Found 3 solutions by greenestamps, ikleyn, MathTherapy:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


(Corrected response -- typo in original response)....

Find the answer using Heron's formula for the area of a triangle in terms of the lengths of the three sides.

A=sqrt%28%28s%29%28s-a%29%28s-b%29%28s-c%29%29

s is the semi-perimeter; a, b, and c are the three side lengths.

In this problem, the perimeter is 54 and one side length is 17. So

let x = second side length
then 54-(17+x) = 37-x = third side length

The semi-perimeter s is 27; the area is

A=sqrt%28%2827%29%2827-17%29%2827-x%29%2827-%2837-x%29%29%29
A=sqrt%28%2827%29%2810%29%2827-x%29%28x-10%29%29

The area is an integer; and all three side lengths are integers.

The expression for the area shows that x is greater than 10 and less than 27; trying different integer values for x (either manually or using some kind of calculator) shows that the other two side lengths are cross%2824%29 25 and cross%2813%29 12.

ANSWER: the length of the longest side is cross%2824%29 25.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
The lengths of the sides of a triangle are positive integers.
One side has length 17 and the perimeter of the triangle is 54.
If the area is also an integer, find the length of the longest side.
~~~~~~~~~~~~~~~~ 

Use the Heron's formula for the area of the triangle

    area = sqrt%28s%2A%28s-a%29%2A%28s-b%29%2A%28s-c%29%29.


Here s = 54/2 = 27 is the semi-perimeter, a = 17, b and c are two other sides.

Since the perimeter is 54 and side "a" is 17, we have  b + c = 54 - a = 54 - 17 = 37.

Let "b" be the longest side of the triangle.

Then  b >= 37/2 = 18.5  and since b is integer, we can write  b >= 19.

Also,  b is less than semi-perimeter b < 54/2 = 27;  c = 37-b.


Then the formula takes the form

    area = sqrt%2827%2A10%2A%2827-b%29%2A%2827-%2837-b%29%29%29 = 3%2Asqrt%282%2A3%2A5%2A%2827-b%29%2A%28b-10%29%29.   (*)


So, we seek for the integer value of "b" in the interval  19 <= b <= 26, which makes 
the right side of expression  (*)  integer number.


   +----------------------------------------------------------+
   |   Then one of the factors (27-b) or (b-10) should be 5,  |
   |                which gives  b = 25.                      |
   +----------------------------------------------------------+


Indeed, then b = 25 is the sought side length, and the area (*) is

    area = 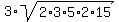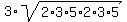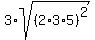3%2Asqrt%282%2A3%2A5%2A2%2A15%29 = 3%2Asqrt%282%2A3%2A5%2A2%2A3%2A5%29 = 3%2Asqrt%28%282%2A3%2A5%29%5E2%29 = 3*2*3*5 = 90 square units.



    Thus the triangle sides are  a= 17,  b= 25  and  c= 37-25 = 12 units; 

                       the longest side is 25 units.

    The triangle inequalities are held, so such triangle does exist.

                 All requirements of the problem are held.



ANSWER.  Such a triangle does exist, and its longest side is 25 units long.

         This solution is a unique :  there is no other solution.

Solved.



Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
The lengths of the sides of a triangle are positive integers. One side has length 17 and the perimeter of the triangle is 54. If the area is also an integer, find the length of the longest side.
Perimeter = 54.
One of the sides = 17. With another side being a, the 3rd side is: 54 - 17 - a = 37 - a 

           Heron's formula: matrix%281%2C3%2C+Area%2C+%22=%22%2C+sqrt%28s%28s+-+a%29%28s+-+b%29%28s+-+c%29%29%29, with: matrix%283%2C3%2C+a%2C+%22=%22%2C+a%2C+b%2C+%22=%22%2C+37+-+a%2C+c%2C+%22=%22%2C+17%29

In addition, .

               We now get: matrix%281%2C3%2C+Area%2C+%22=%22%2C+sqrt%28s%28s+-+a%29%28s+-+b%29%28s+-+c%29%29%29
                                  

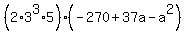In order for the area to be an INTEGER, the RADICAND, %282%2A3%5E3%2A5%29%28-+270+%2B+37a+-+a%5E2%29 needs to be a PERFECT SQUARE. As such, the 2(3)3(5), or 270
needs to be MULTIPLIED by one MORE 2, one MORE 3, and one MORE 5, or 2(3)(5), in order to make it 22(34)(52), or 8,100 (PERFECT SQUARE). 
This means that 
                 (a - 25)(a - 12) = 0
   a - 25 = 0      or      a - 12 = 0
        a = 25     or           a = 12

So, if a = 25, then b = 37 - 25 = 12, and c = 17 (given)
    if a = 12, then b = 37 - 12 = 25, and c = 17 (given)

Either way, with the 3 sides being 25, 12, and 17, the longest side of the triangle is 25.