Question 1198962: Lines drawn parallel to the base of the triangle pictured, separate the other two sides into 10 equally spaced parts. What percentage of the triangle is grey?
Found 3 solutions by Alan3354, lotusjayden, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by lotusjayden(18)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The area of the k-th triangle is 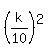 of the area of the greatest triangle, A.
Therefore, the area of k-th individual single shape is of the area of the greatest triangle, A.
Therefore, the area of k-th individual single shape is
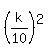 - - 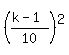 of the area of greatest triangle, A, (1)
or of the area of greatest triangle, A, (1)
or
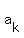 = = 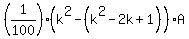 = =  . (2)
From here, the area of the grey part is
A(grey) = . (2)
From here, the area of the grey part is
A(grey) = 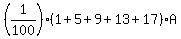 = = 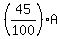 . (3)
(summing all (2k-1) over k = 1, 3, 5, 7, 9)
The area of the unshaded (white) part is
A(white) = . (3)
(summing all (2k-1) over k = 1, 3, 5, 7, 9)
The area of the unshaded (white) part is
A(white) = 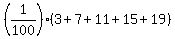 = = 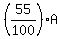 . (4)
(summing all (2k-1) over k = 2, 4, 6, 8, 10)
Therefore, the ratio under the problem's question is . (4)
(summing all (2k-1) over k = 2, 4, 6, 8, 10)
Therefore, the ratio under the problem's question is
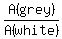 = = 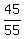 = = 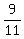 . ANSWER . ANSWER
Solved.
------------
Surely, one can avoid calculating unshaded area (4), when the area of grey part (3) is just calculated.
I did it only for the purpose of completeness.
|
|
|