Question 1197163: If −𝜋 ≤ 𝑥 ≤ 0, then cos−1(cos 𝑥) is:
A)𝑥 B)𝜋−𝑥 C)2𝜋+𝑥 D)2𝜋−𝑥 E)None
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you graph the equation, you can see what's going on.
the graph is shown below:
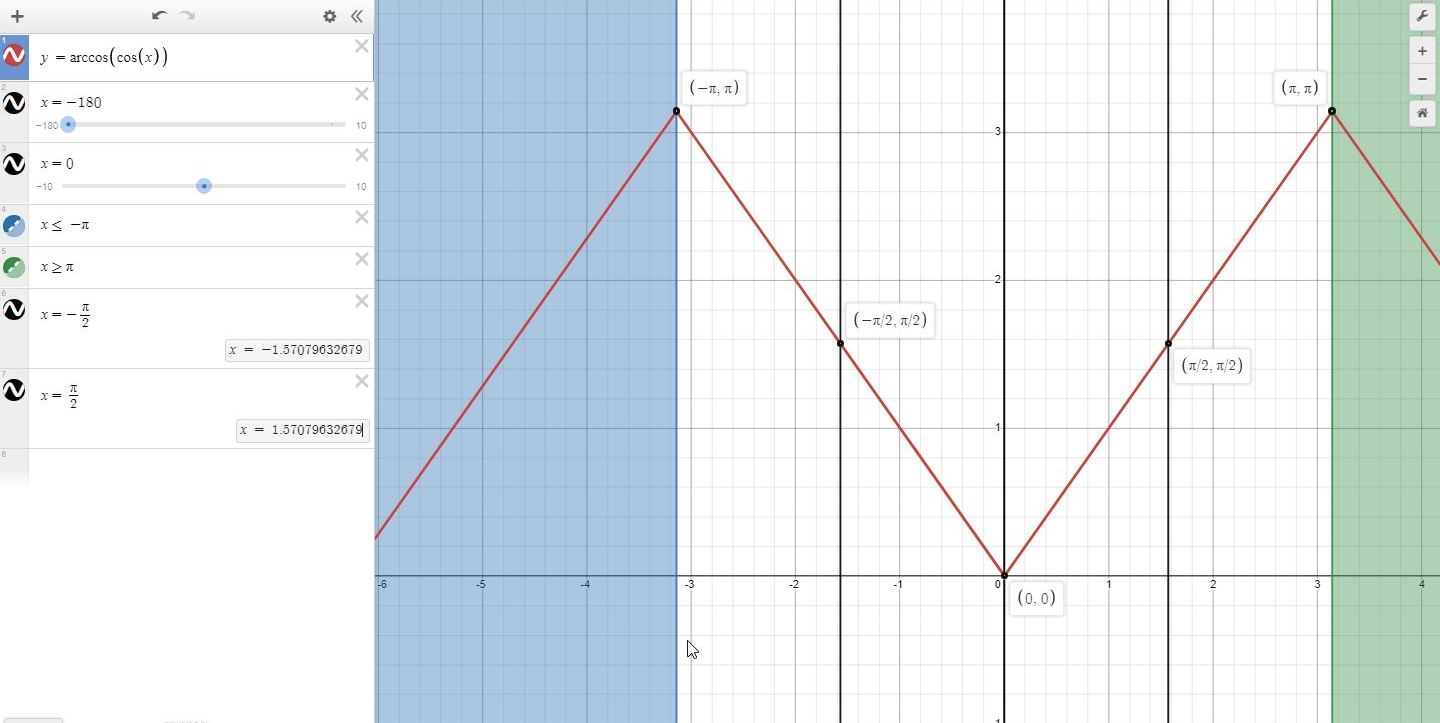
you can see from the graph that when x = pi/2, y = arccos(cos(x)) = arccos(cos(pi/2)) = pi/2.
that would indicate that arccos(cos(x)) = x.
that's true when 0 < x < pi.
arccos(cos(-pi/2)) = pi/2 as well.
however, since the angle is -pi/2, then the coordinate pair is (-pi/2,pi/2) which indicates that arccos(x) = -x when -pi < x < 0
the equivalent positive angle of -x is equal to -pi/2 + 2pi = 3pi/2.
that would be 2pi + x because 2pi + (-pi/2) = 3pi/2.
this is very tough to see unless you can graph it.
the graphing software i used is at https://www.desmos.com/calculator
it looks to me that your solution is selection C which is 2pi + x.
you didn't have -x as a solution.
you needed to now that -x was equivalent to 2pi - (-x) = 2pi + x.
arccos(cos(-pi/2) = pi/2.
arccos(cos(2pi+pi/2) = pi/2.
let me know if you have any questions.
theo
Answer by greenestamps(13241)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For the inverse cosine function, the input is a real number between -1 and +1, and the output value is in a range which is the interval closest to 0 in which cos(x) takes on all it values.
cos(x) takes on all its values on [0,pi), so the output of the inverse cosine function is on that interval. Note cos(x) also takes on all its value on [-pi,0); but the convention is to use the interval where the numbers are positive.
cos(x) has a period of 2pi, so cos^(-1)(cos(x)) returns a value equal to x, plus or minus the multiple of 2pi that makes the output value between 0 and pi.
Since in this problem the input value x is between -pi and 0, the output value needs to be x+2pi.
ANSWER: C
|
|
|