Question 1194922: the tangent and normal to the curve y=4*sqrt(x+2) at the point P(7,12) cut the x-axis at M and N respectively. Calculate the area of the triangle PMN
Found 2 solutions by math_helper, greenestamps:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Red = 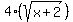 = f(x) = f(x)
Blue = normal
Green = tangent
 . .
Tangent line:
dy/dx = 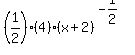 = = 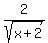
This is the slope of the tangent line. Using the fact that the tangent meets the function f(x) at (7,12) let's us find the y-intercept:
At x=7, dy/dx = 
Now, y = (2/3)x + b
12 = (2/3)*7 + b ==> b = 22/3
You can now write y = (2/3)x + 22/3 for the tangent line
Set y=0 to find the x-axis crossing:
0 = (2/3)x + 22/3
Solving for x gives x = -11
From this, we conclude M is at (-11,0)
Normal line:
The slope of the normal line will be -1/(slope of tangent). We are only interested in (7,12), so slope of normal is -(1/(2/3)) = -3/2
You can now write y = (-3/2)x + b for the normal line
Use the fact that the normal line also passes through (7,12) to find
the y-intercept of the normal:
12 = (-3/2)(7) + b ==> solve for b ==> b = 45/2
We can now write y = (-3/2)x + 45/2 for the normal line
Now find the x-axis crossing by setting y=0:
0 = (-3/2)x + 45/2 ==> solve for x ==> x = 15
So N is at (15, 0)
Area of PMN:
P is at (7,12) so you can calculate |PN| and |PM| ... and then use the triangle area formula A = (1/2)|PN| * |PM|
I got 156.00 sq units when I did these calculations.
Answer by greenestamps(13198)   (Show Source): (Show Source):
|
|
|