SOLUTION: A 5-12-13 triangle is inscribed in a circle, which is inscribed in a larger 5-12-13 triangle. What is the ratio of the area of the smaller triangle to the area of the larger triang

Let the smaller 5-12-13 triangle be ABC with the side lengths of 5, 12 and 13 units.


This triangle is a right angled triangle (the fact widely known, since 5^2 + 12^2 = 169 = 13^2).


Since this triangle ABC is inscribed in the circle, the hypotenuse of the length 13 units is the DIAMETER of the circle.

Thus the radius of the circle is  13/2 = 6.5 units.


Next, since the larger triangle has the same ratio of the sides, 5:12:13, the larger triangle is SIMILAR
to the smaller triangle; in particular, the larger triangle is a right-angled triangle, too.


Let the similarity coefficient be k, from larger to smaller, so the sides of the larger triangle
be  a= 5k,  b= 12k  and  c= 13k.


Then the radius of circle, inscribed in the larger triangle be

    r =  =  =  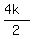= 2k.


But we just know that this radius is 6.5 units (see the reasonings above).


It gives us an equation

    2k = 6.5,  which implies  k = 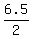 = 3.25.


Thus the similarity coefficient is k= 3.25 from larger triangle to smaller, 
or 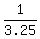   from smaller to larger.


Hence, the ratio of the area of the smaller triangle to the area of the larger triangle is

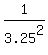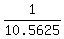     =  = 0.09467  (rounded).      ANSWER