Question 1169194: Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b), and sqrt(c). What about a^2, b^2, and c^2?
Answer by ikleyn(52924)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b), and sqrt(c).
~~~~~~~~~~~~
Proof
Let assume that
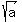 + + 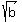 <= <=  . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, square both sides of (1). You will get
a + . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, square both sides of (1). You will get
a +  + b <= c, or
a + b <= c - + b <= c, or
a + b <= c -  .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES 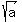 + + 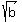 > >  .
It works for any combinations of sides of a triangle.
Thus we proved that the values .
It works for any combinations of sides of a triangle.
Thus we proved that the values 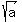 , , 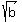 , ,  satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then 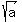 , , 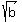 , and , and  form a triangle, too. form a triangle, too.
************************
S O L V E D
************************
|
|
|