Question 1151945: a triangle has an area of 10 square units and enclosed by the x-axis, y-axis and the line 2y+ax-10=0. Find the values of a
Found 2 solutions by rothauserc, MathLover1:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! solve the line equation for y
:
y = -ax/2 +5
:
therefore, the y-axis intercept is 5
:
area of triangle = (1/2) * base * height
:
(1/2) * base * 5 = 10
:
base = 4 which is the x-axis intercept
:
-a(4)/2 +5 = 0
:
-2a = -5
:
a = 5/2
:
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website! a triangle has an area of  square units and enclosed by the  -axis,  -axis and the line 
Find the values of 
given:
a triangle has an area of
 is y-axis, and  is x-axis.
=> if  },
 =>y-intercept is at ( , )=> one leg of triangle (height) is
 => if }
=> => the other leg of triangle, x- intercept is at ( ,)
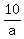since a triangle has an area of , we have
and, your equation is:
then x- intercept is at (,)=( ,)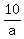
check the area:
|
|
|
