Question 1143115: Three sides of a triangle measures 12 cm, 18 cm and 10 cm. Find the altitude of the longest side, the median of the longest side, the length of angle bisector of the largest angle and the line segment joining the midpoints of 12 cm and 18 cm sides. Thanks.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
(a) To find the area of the triangle, use the Heron's formula.
On the Heron's formula, see the lessons
Proof of the Heron's formula for the area of a triangle
One more proof of the Heron's formula for the area of a triangle
in this site.
The semi-perimeter is equal to s =  = 20 cm.
The area of the triangle is (Heron's formula)
A =  =  =  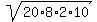=  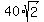= 56.57 cm^2 (approximately). ANSWER
(b) Altitude to the longest side.
Let h be the altitude to the longest side.
Then for the area of the triangle,
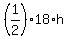A =  = 56.57 cm^2,
which implies
h = 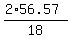 = 6.29 cm (approximately). ANSWER
(c) The median to the longest side.
In a triangle with the sides "a", "b" and "c", the median drawn to the side "c" has the length of
 =  .
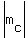For this theorem, see the lesson
The length of a median of a triangle
in this site.
Substitute the given data a= 12, b= 10, c= 18 to get the length of the median drawn to the side of the length 18 cm
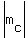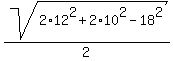=  =  = 6.403 cm. ANSWER
d. The length of angle bisector of the largest angle of the triangle.
If the triangle is not isosceles, then this problem (this question) is FAR BEYOND any school Math curriculum.
e. The line segment joining the midpoints of 12 cm and 18 cm sides
It is called "the mid-segment" of the triangle.
It is widely known that the mid-segment length is half of the length of the parallel side of the triangle.
So, the answer is  = 5 cm in this case.
/\/\/\/\/\//\\/\/\/\/
My advise to you for the future:
Do not include so many questions in your posts.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
(1) length of the altitude to the longest side...
As shown by tutor @ikleyn, the area of the triangle, from Heron's formula, is  .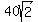
Given that area and the length of the base 18, the height is calculated from the most common formula for the area of a triangle:
Use Stewart's Theorem to find the lengths of the median to the longest side and the length of the bisector of the largest angle.
Here is an ugly text description....
(See the wikipedia article on Stewart's Theorem for a diagram)
Let the base of the triangle be BC (length a). Then side AC has length b and side AB has length c. P is any point on base BC; d is the length of AP. Let CP=n and BP=m. Then the theorem relates the lengths of all the segments as follows:
Note the formula is usually written using b^2, c^2, and d^2. I like the format I showed because, in applying the theorem, it gives you a visual picture of the relationship between the calculations "bmb", "cnc" and "dad".
(2) length of the median to the longest side...
You know m=n=9 because AP is the median. The length of the median, d, is the only unknown. Plug in the known values and solve for d.
(3) length of the angle bisector of the largest angle...
The angle bisector divides the base 18 into two pieces whose lengths are in the same ratio as the lengths of the two sides that form the angle. Divide 18 into two parts in the ratio 10:12 to find the values of m and n; then perform the same calculation as above with the new values for m and n.
(4) length of the segment joining the midpoints of the 12cm and 18cm sides....
This is by far the easiest of the problems -- it is half the length of the 10cm side.
|
|
|
