.
If triangles are similar, then their corresponding side lengths are proportional.
In triangle ABC, the sides are AB, BC and AC.
In triangle DEF, the corresponding sides are DE, EF and DF.
You are given |AB| = 3 (the length of AB), |BC| = 5 and |AC| = 7.
|DE| = 6.
They want you find |EF| and |DF|.
For |EF|, you have this proportion
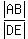 =
= 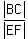 , or
, or  =
= 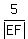 ,
which implies |EF| =
,
which implies |EF| = 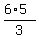 =
= 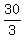 = 10.
For |DF|, you have this proportion
= 10.
For |DF|, you have this proportion
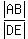 =
= 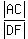 , or
, or  =
=  ,
which implies |EF| =
,
which implies |EF| = 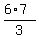 =
= 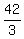 = 14. ANSWER
= 14. ANSWER
Solved. The solution is completed.
----------------
Since the corresponding side DE of the triangle DEF is twice the side AB of the triangle ABC, you may conclude from similarity
that all other sides of the triangle DEF are twice the corresponding sides of the triangle ABC, and complete the solution with it.
It would be using the same proportions without pronouncing this term.
-----------------
Is everything clear to you ?
If not, then let me know.
If you will post your question/questions to me, then please refer to the ID number of this problem, which is 1138874.
(Otherwise, I will not know to whom to answer).
Happy learning !