Question 1138457: 1. Find the largest angle of the triangle whose sides are of length 2cm, 4cm,
5cm.
2. If sin x =3/5 and x is acute,find the value of tan 2x and tan x/2.
3. Find all the angles 0° and 360° whose sine is +.5.
4. Find all the angles between 0° and 360° whose tangent is 1.5.
5. By means of a right-angle isosceles ∆, deduce that
Sin 45°=cos45°=1/√2.
Prove that cos(45°+A)=1/√2(cosA-sinA) and sin(45°+A)=1/√2(cosA+sinA).
Deduce cos A = 1/√2{cos(45°+A)+sin (45° + A)} and the corresponding result
for sin A.
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! 1. Find the largest angle of the triangle whose sides are of length 2cm, 4cm,
5cm.
The largest angle is opposite the longest side.
Use the Cosine Law.
---------------------
2. If sin x =3/5 and x is acute,find the value of tan 2x and tan x/2.
3. Find all the angles 0° and 360° whose sine is +.5.
you have to know that.
-------
4. Find all the angles between 0° and 360° whose tangent is 1.5.
Use a calculator to find the angle in Q1.
Then add 180 degs for the angle in Q3.
-----------
5. By means of a right-angle isosceles ∆, deduce that
Sin 45°=cos45°=1/√2.
Prove that cos(45°+A)=1/√2(cosA-sinA) and sin(45°+A)=1/√2(cosA+sinA).
Deduce cos A = 1/√2{cos(45°+A)+sin (45° + A)} and the corresponding result
for sin A.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! 1. The largest angle of the triangle whose sides are of length 2cm, 4cm,
5cm is the one opposite the longest (5-cm) side.
To find that angle we have to use law of cosines, which says that in a triangle with sides a, b, and c, and angle A opposite side a,
If A is a right angle, then  , and that equation turns into the  (the Pythagorean theorem). Otherwise, as in this case, the 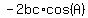 "correction" makes a larger for obtuse angles (as in this case), and smaller for acute ones.
So, for this case we find  opposite  (cm) , and the other two side lengths are b and c.
2. If  and x is acute, x is the smallest angle of a right triangle with sides measuring 3, 4, and 5:
 So,  and  .
From there, I can find, in a list of trigonometric identities,
 and  ,
and calculate
 , and
3. Find all the angles between 0° and 360° whose sine is +.5.
We know that  , and we know that in each quadrant
The function sine takes values from 0 to 1, or 0 to -1.
In the whole first counterclockwise turn, between 0° and 360°,
there is only one angle whose sine is 1  (and only one angle whose sign is -1), but all other positive values happen twice,
once as sine goes from 0 to 1 in the first quadrant, and again as sine goes from 1 back to 0 in the second quadrant.
Suplementary angles  and  have the same 0.5 sine.
|
|
|
