Question 1082130: From a point outside the equilateral triangle, the distances of the 10, 10, and 18. Find the dimension of the triangle.
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From a point outside the equilateral triangle, the distances  are 10, 10, and 18 units. Find the dimension of the triangle. are 10, 10, and 18 units. Find the dimension of the triangle.
~~~~~~~~~~~~~~~~~~~
0. Make a sketch to follow my arguments.
Let the triangle will be ABC, and the point outside be D.
Connect D by segments with A, B and C.
Let CD = 10, BD = 10 and AD = 18.
Let the length of the side of the triangle ABC be x.
1. The quadrilateral ACBD is a kite, since AB = AC and BD = CD.
Therefore, AD is the angle bisector to angles A and D.
It implies that the angle DAB is 30 degs.
2. Now consider the triangle ABD
Its side AD is 18 units long, side BD is 10 units long and side AB is x.
The angle DAB is 30 degs.
Apply the Cosines law theorem:
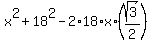 = = 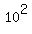 , or , or
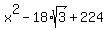 = 0.
It is your quadratic equation to find x. = 0.
It is your quadratic equation to find x.
The setup is done. The rest is just arithmetic.
I got the answer x = 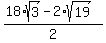 . .
|
|
|