SOLUTION: Point P which is 10 cm distance from the vertices of a triangle with sides 4,5, and 6. Find the distance from point P to the plane of the triangle.

Use the formula for the volume of pyramid

V = ,

where V is the volume, S is the base area, and h is the altitude drown to the base.

In your case the altitude is exactly the distance you need.


For the volume of the tetrahedron, there is a formula expressing the volume via the tetrahedron's edge lengths.

You can find this formula in Wikipedia https://en.wikipedia.org/wiki/Tetrahedron 
or in other sources. 


For the area of the base you can use the Heron's formula.

In this way you are able to get the answer.


You can even find a free of charge calculator for the volume of a tetrahedron in the Internet and calculate the volume from there.

Consider the plane of the triangle and the sphere of the radius R = 10 cm with the center at the point P.
This plane cuts the sphere and the triangle lies in/at the cutting section.

Now what you need is to find the radius "r" of the circle circumscribed about the triangle.  

Then the distance from the point P to the plane is 

d = 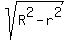.     (1)


For the radius of the circle circumscribed about the triangle, there is the formula

r = 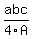,         (2)

where a, b, and c are the triangle's side dimensions and A is its area.

See the lesson Proof of the formula for the radius of the circumscribed circle in this site.


To calculate the area, use the Heron's formula

A =   (where s is semi-perimeter) = 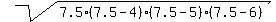 =  = 9.922 cm^2 (approximately). 


Then according (2)  r = 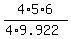 = 3.024 cm (approximately).


Then the distance from P to the plane (which is the value under the question) is 

d = 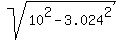 = 9.532 cm.