Question 1035508: I have an equilateral triangle with
Base: 35
Mid segment: 20
Side below mid: 12
I need to find the segment length above the mid-segment. Please help.
Answer by KMST(5330)   (Show Source): (Show Source):
You can put this solution on YOUR website! A midsegment is a segment parallel to one side of a triangle,
connecting the midpoints of the other two sides.
We like to draw the midsegment and the side parallel to it as horizontal segments, and we like to call that side the base, like this:
 Since the midsegment connects midpoints of the sides, it divides each sides into two segments of equal length. Since the midsegment connects midpoints of the sides, it divides each sides into two segments of equal length.
Also, all triangle midsegments are half as long as the base.
I do not know what your drawing looks like, but I believe the words "equilateral" and "midsegment" do not belong in your problem.
I will take a guess about what your problem really is, and I will answer the guessed problem.
The drawing below shows what a triangle would look like with
a base length of 35,
a segment parallel to the base measuring 20, and
a side divided by the midsegment into segments of length  and and  : :

It can be made by superimposing the two similar triangles in the drawings below:
  
We know that the triangles are similar because the corresponding angles have the same measures (or as the teacher says, "are congruent").
The vertex (top) angle is the same angle,
and the base angles are congruent because are corresponding angles formed by a transversal with two parallel lines.
The length of the sides in similar triangles are in the same scaling factor ratio, so
 or, or,
multiplying both sides of the equal sign times  , ,
 , and multiplying both sides times , and multiplying both sides times  , we get , we get
 , so , so
 ---> --->  ---> --->  ---> --->  . .
So, the side measuring 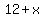 measures measures  , ,
which means that the triangle is not equilateral.
|
|
|