SOLUTION: if triangles EFG and LNM are right triangles and they are also similar what is the measure of F, I know that angles E and L go together and angles F and N go together and that angl

Algebra ->  Triangles -> SOLUTION: if triangles EFG and LNM are right triangles and they are also similar what is the measure of F, I know that angles E and L go together and angles F and N go together and that angl      Log On


   

Question 1019262: if triangles EFG and LNM are right triangles and they are also similar what is the measure of F, I know that angles E and L go together and angles F and N go together and that angles G and M go together it then says to let G=8 1/10 N=2 1/2 and M=16 1/5 what is the measure of angle F
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!

my diagram of your triangles formed is shown below:

$$$

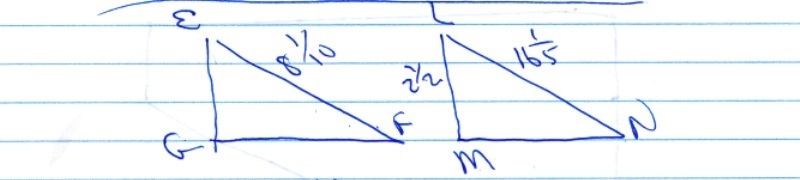
since the triangles are similar, then:

angle N = angle F.

angle L = angle E.

angle M = angle G

i'm assuming that angles M and G are the right angles of their respective triangles.

this makes sides EF and LN the hypotenuse of their respective triangles.

in triangle EFG, i'm assuming that side E is opposite angle E, side F is opposite angle F, side G is opposite angle G.

in triangle LNM, i'm assuming that side L is opposite angle L, side N is opposite angle N, side M is opposite angle M.

this is the normal way that sides and angles of triangles are related to each other.

you are given that side G = 8 and 1/2, side N = 2 and 1/2, side M = 16 and 1/5.

under this assumption, the diagram marks the length of each side given.

you are asked to find the measure of angle F.

since the triangle are similar, then the measure of angle F is equal to the measure of angle N.

the sine of angle N is equal to the side opposite angle N divided by the hypotenuse.

this would be side N divided by side M.

in the diagram, side N is shown as the line segment LM and side M is shown as the line segment LN.

since the measure of side N is eual to 2 and 1/2, and the measure of side M is equal to 16 and 1/5, and since side N is opposite angle N, and since side M is the hypotenuse of the triangle LNM, then:

sine of angle N = opposite / hypotenuse = side N / side M = (2 and 1/2) / (16 and 1/5).

use your calculator to find the sine of angle N is equal to .1543209877.

angle N is therefore equal to the arcsine of .1543209877.

that makes angle N equal to 8.877417897 degrees.

since angle F is equal to angle N, then angle F is equal to 8.77417897 degrees as well.