Question 1009174: Show that the point (6,6),(2,3) and (4,7) are the vertices of a right angled triangle
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by ikleyn(52920)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that the point (6,6), (2,3) and (4,7) are the vertices of a right angled triangle.
----------------------------------------------------------------------
Calculate the three segments in the coordinate plane that are sides of the triangle.
For example, one segment, connecting the points (6,6) and (2,3), is (6-2,6-3) = (4,3).
Its length is  = =  = 5.
Two other segments are (2,-1) and (2,4).
Their lengths are = 5.
Two other segments are (2,-1) and (2,4).
Their lengths are 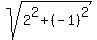 = =  and and 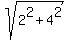 = =  .
Now notice that .
Now notice that  = 25 and = 25 and 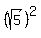 + + 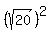 = 5 + 20 = 25.
It is just enough to state that the triangle is right-angled.
The point (4,7) is the vertex of the right angle. = 5 + 20 = 25.
It is just enough to state that the triangle is right-angled.
The point (4,7) is the vertex of the right angle.
|
|
|