First, a little background, so you can understand what's going on:
Two digit numbers are always equal to
10 times their first digit plus their second digit.
For instance,
23 has first digit 2 and second digit 3. (10 times 2) plus 3 = 20+3 = 23
74 has first digit 7 and second digit 4. (10 times 7) plus 4 = 70+4 = 74
11 has first digit 1 and second digit 1. (10 times 1) plus 1 = 10+1 = 11
So in general:
"FS" has first digit F and second digit S. (10 times F) plus S = 10F+S
If you swap the dgits from "FS" to "SF",
"SF" has first digit S and second digit F. (10 times S) plus F = 10S+F
--------------------------------------
Now for the problem:
Let F = first digit and S = second digit.
So the number = 10F + S
When you swap (reverse) the digits, the new number is 10S + F
The sum of the digits in a two digit number is 12.
So the first equation is this:
F + S = 12
The new number obtained when the digits are reversed is 36 more than the original number.
So




 So the second equation is
So the second equation is
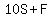

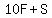

 Let's simplify that:
Let's simplify that:
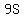

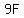

 and simplify it further by dividing through by 9
and simplify it further by dividing through by 9




 So you have this system of equations:
So you have this system of equations:
 Using the second equation, substitute F+4 for S in the
first equation F+S = 12
F+(F+4) = 12
F+F+4 = 12
2F+4 = 12
2F = 8
F = 4
Substitute 4 for F in S=F+4
S=4+4
S=8
So the first digit F is 4 and the second digit S is 8
So the number is 48.
Now let's check:
Using the second equation, substitute F+4 for S in the
first equation F+S = 12
F+(F+4) = 12
F+F+4 = 12
2F+4 = 12
2F = 8
F = 4
Substitute 4 for F in S=F+4
S=4+4
S=8
So the first digit F is 4 and the second digit S is 8
So the number is 48.
Now let's check:
The sum of the digits in a two digit number, 48 is 12.
That checks because 4+8 = 12
The new number obtained when the digits are reversed, which is 84,
is 36 more than the original number.
That checks because 84 is 36 more than 48, because when 36 more than
48 is 48+36 = 84.
So 48 is the correct answer.
[Your teacher probably uses t and u instead of F and S, and says
"tens digit" instead of "First digit" and "ones or units digit" instead
of second digit.]
Edwin