SOLUTION: I have two equations, one is a hyperbola and one is a straight line. The line is in the form of {{{ y+kx=-2 }}}. I am not sure what exactly the hyperbola equation was as it is not

Algebra ->  Systems-of-equations -> SOLUTION: I have two equations, one is a hyperbola and one is a straight line. The line is in the form of {{{ y+kx=-2 }}}. I am not sure what exactly the hyperbola equation was as it is not       Log On


   

Question 857921: I have two equations, one is a hyperbola and one is a straight line. The line is in the form of +y%2Bkx=-2+. I am not sure what exactly the hyperbola equation was as it is not written down, but it was in a form similar to +y%28x%2B8%29=x+. The problem explains that the hyperbola is the edges of two circular pools and the line is the path that goes between them. The problem states 'find the appropriate values of k' so that the path does not cross into the pools, that is, no intercepts between the line and the hyperbola. I have managed to substitute the equations together to get +x%2F%28x%2B8%29=%28-kx-2%29+. This can be turned into the quadratic equation +kx%5E2%2Bx%283%2B8k%29%2B16=0+. 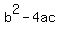Since the aim is to find appropriate values of k that make the line not cross through the hyperbola, the discriminant ( b%5E2-4ac+ ), must be equal to less than 0 to show that there are no real roots/solutions. 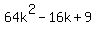By substituting the a, b and c values from this quadratic equation into the discriminant, another quadratic equation is created: +64k%5E2-16k%2B9+. This needs to equal less than 0 for the line to not pass through the hyperbola.
I am confused as to what to do from here to find appropriate values of k and if I have done the previous steps correctly. I am sure that I am close to solving it.
The second part of this question also states, find the range of possible values. Although, I first need to figure out how to solve the first part of the question.
Please help if you can, I have literally been trying to figure this out for hours.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You are on the right track, but you probably have the hyperbola equation wrong.
If the equation of the hyperbola is really +y%28x%2B8%29=x+ there is no solution.
To get no intercepts between the line and the hyperbola,
the equation +kx%5E2%2Bx%283%2B8k%29%2B16=0+ must have no real solutions.
That would require the discriminant to be negative,
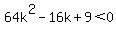
+64k%5E2-16k%2B9+%3C0
The problem is that f%28k%29=64k%5E2-16k%2B9 is always positive.
64k%5E2-16k%2B9=0 has no solutions.
f%28k%29=64k%5E2-16k%2B9=64k%5E2-16k%2B1%2B8=%288k%2B1%29%5E2%2B8%3E=8

If you have the vertices and foci of the hyperbola, you can graph a box and a pair of asymptotes.
If your line crosses the asymptotes inside that box, it would not intersect the hyperbola.
On the other hand, if one point of the line is "on the wrong side of the tracks",
on the same side of one of the branches of the hyperbola as the corresponding focus,
then the line will cross the hyperbola.
+y%28x%2B8%29=x+<-->+y%28x%2B8%29=%28x%2B8%29-8<-->y%28x%2B8%29-%28x%2B8%29=-8<-->%28y-1%29%28x%2B8%29=-8 has asymptotes x=-8 and y=1 .
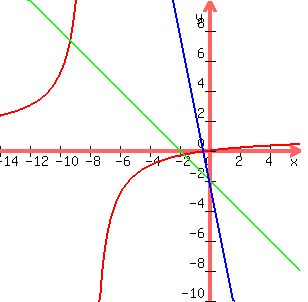graph%28300%2C300%2C-14%2C6%2C-10%2C10%2Cx%2F%28x%2B8%29%2C-x-2%2C-5x-2%29 Any y%2Bkx=-2 , like the blue and green lines, will go through point (0,-2), and will cross the hyperbola.