I need help with this equation:
It's not an equation, but an inequality.
(x-5)exp-5<_0 does the negative 5 exponent tell me that there may be no solution?
No, not at all!
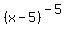 < 0
just means:
< 0
just means:
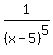 < 0, undefined for x = 5
Now we take the fifth root of
both sides. Remember there is only
one real odd root of any real number,
regardless of whether the number under
the radical is is positive, negative,
or zero. The same can't be said for
even roots, but we don't have to worry
about them here since 5th root is an
odd root.
< 0, undefined for x = 5
Now we take the fifth root of
both sides. Remember there is only
one real odd root of any real number,
regardless of whether the number under
the radical is is positive, negative,
or zero. The same can't be said for
even roots, but we don't have to worry
about them here since 5th root is an
odd root.
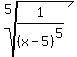 <
< 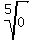 , undefined for x = 5
, undefined for x = 5
 <
<  , undefined for x = 5
There is no value of x for which
, undefined for x = 5
There is no value of x for which  =
=  , therefore
we may as well write:
, therefore
we may as well write:
 <
<  , undefined for x = 5
Then we know that a number is positive if and only if its reciprocal
is positive, and negative if and only if its reciprocal is negative.
So x - 5 < 0 or
x < 5
The graph of that looks like this:
<=========================o------------------>
-3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
The solution is set-builder notation is
{x|x < 5}
Or in interval notation: (-oo, 5)
The graph of the left side of the original
inequality
y =
, undefined for x = 5
Then we know that a number is positive if and only if its reciprocal
is positive, and negative if and only if its reciprocal is negative.
So x - 5 < 0 or
x < 5
The graph of that looks like this:
<=========================o------------------>
-3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
The solution is set-builder notation is
{x|x < 5}
Or in interval notation: (-oo, 5)
The graph of the left side of the original
inequality
y = 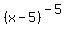 is this
is this  The curve is always below the x-axis when x is less than 5
and always above the x-axis when x is greater than 5. I agree
it looks as if it touches the x-axis, but it doesn't really.
It just comes so close to it that it can only be drawn looking
as though it touches it but it doesn't. There is a vertical
asymptote at x = 5 as you see. There is no value of x
that will produce equality, hence this convinces us that the
interval notation
(-oo, 5) is the correct solution.
Edwin
The curve is always below the x-axis when x is less than 5
and always above the x-axis when x is greater than 5. I agree
it looks as if it touches the x-axis, but it doesn't really.
It just comes so close to it that it can only be drawn looking
as though it touches it but it doesn't. There is a vertical
asymptote at x = 5 as you see. There is no value of x
that will produce equality, hence this convinces us that the
interval notation
(-oo, 5) is the correct solution.
Edwin