We'll solve the system:


by elimination by addition.To eliminate by addition, we need to set both coefficients of x to numbers with changed signs, i.e a and -a. Since in the second equation we have 5 as our coefficient for x, to get -2 we have to multiply all terms of the second equation by 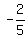 which is equal to -0.4. which is equal to -0.4.
Multiplying, we get on our second equation:

Adding both equations we get:

Since 2 and -2 cancel out, we have a linear equation:Therefore, we know that y = -3.
Plugging that in into the first equation gives us:







Therefore, our answer is:
 |