Line them up so the letters, signs and equal signs are in columns:
equation 1: 4x + 2y - 6z = -38
equation 2: 5x - 4y + z = -18
equation 3: x + 3y + 7z = 38
We choose the equation 1 and 2 to eliminate y from.
If we multiply equation 1 by 2 the 2y will become 4y
and cancel with the -4y in equation 2:
We multiply equation 1 by 2 and write equation 2 under it
and add them term by term and call it equation 4:
8x + 4y - 12z = -76
equation 2: 5x - 4y + z = -18
-----------------------------------
equation 4: 13x - 11z = -94
Now we have to use the unused equation 3 with either of
the equations we just used, 1 or 2, and eliminate that
SAME variable, y. I will pick equations 1 and 3
equation 1: 4x + 2y - 6z = -38
equation 3: x + 3y + 7z = 38
To eliminate y, we must make the y-terms cancel out.
Their coefficients are 2 and 3. The smallest whole
number 2 and 3 will both go into is 6. So we want
to make the 2y term into +6y and the 3y term into -6y.
So we multiply equation 1 by 3 and equation 2 by -2, and
add them term by term, and call it equation 5:
12x + 6y - 18z = -114
-2x - 6y - 14z = -76
----------------------
equation 5 10x - 32z = -190
Now we take equations 4 and 5:
equation 4: 13x - 11z = -94
equation 5 10x - 32z = -190
Notice that equation 5 can be divided through by 2.
That will make it a little easier. We'll call it equation 6.
equation 4: 13x - 11z = -94
equation 6: 5x - 16z = -95
We'll pick one of the letters x or y to eliminate.
Let's pick x to eliminate. To eliminate x, we must
make the x-terms cancel out. Their coefficients are
13 and 5. The smallest whole number 13 and 5 will
both go into is 65. So we want to make the 13x term
into +65x and the 5x term into -65x.
So we multiply equation 4 by 5 and equation 6 by -13, and
add them term by term, and solve for y:
65x - 55z = -470
-65x + 208z = 1235
------------------
153z = 765
z = 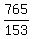 z = 5
Now we substitute z = 5 into equation 5 or 6. We'll
choose equation 6:
equation 6: 5x - 16z = -95
5x - 16(5) = -95
5x - 80 = -95
5x = -15
x =
z = 5
Now we substitute z = 5 into equation 5 or 6. We'll
choose equation 6:
equation 6: 5x - 16z = -95
5x - 16(5) = -95
5x - 80 = -95
5x = -15
x = 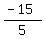 x = -3
Finally we substitute x = -3 and z = 5 into any one
of the original equations 1,2, or 3. We'll choose
equation 1:
equation 1: 4x + 2y - 6z = -38
4(-3) + 2y - 6(5) = -38
-12 + 2y - 30 = -38
-42 + 2y = -38
2y = 4
y =
x = -3
Finally we substitute x = -3 and z = 5 into any one
of the original equations 1,2, or 3. We'll choose
equation 1:
equation 1: 4x + 2y - 6z = -38
4(-3) + 2y - 6(5) = -38
-12 + 2y - 30 = -38
-42 + 2y = -38
2y = 4
y =  y = 2
So the solution is (x,y,z) = (-3,2,5)
Edwin
y = 2
So the solution is (x,y,z) = (-3,2,5)
Edwin