SOLUTION: The equation x3 +3xy + y3 = 1 is solved in integers. Find the possible values of x-y

Algebra ->  Systems-of-equations -> SOLUTION: The equation x3 +3xy + y3 = 1 is solved in integers. Find the possible values of x-y      Log On


   

Question 549954: The equation x3 +3xy + y3 = 1 is solved in integers. Find the possible values of x-y
Found 3 solutions by Alan3354, Edwin McCravy, richard1234:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
(0,1) & (1,0)

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
Wow! The other tutor didn't solve anything.  I don't know where he got that.

The equation x³ + 3xy + y³ = 1 is solved in integers. Find the possible values
of x-y.

x³ + 3xy + y³ - 1 = 0
 
We must factor that!  That's gonna be tough:

Let's try to factor this in the form:
 
(Ax + By + C)(Dx² + Ey² + Fxy + Gx + Hy + I) = 0
 
where, A,B,C,D,E,F,G,H, and I are all integers
 
Then this must be an identity
 
x³ + 3xy + y³ - 1 = (Ax + By + C)(Dx² + Ey² + Fxy + Gx + Hy + I)  
 
The coefficient of x³ on the left is 1.  
The coefficient of x³ on the right is AD
So AD = 1
 
The coefficient of x² on the left is 0.  (Since there are no terms in x²)  
The coefficient of x² on the right is AG + CD
So AG + CD = 0
 
The coefficient of xy on the left is 3.   
The coefficient of xy on the right is AH + BG + CF
So AH + BG + CF = 3
 
The coefficient of y³ on the left is 1.  
The coefficient of y³ on the right is AD
So BE = 1
 
The coefficient of x on the left is 0.  (Since there are no terms in x)  
The coefficient of x on the right is AI + CG
So AI + CG = 0
 
The coefficient of y on the left is 0.  (Since there are no terms in y)  
The coefficient of y on the right is BI + CH
So BI + CH = 0
 
The constant term on the left is -1,
The constant term on the right is CI
So CI = -1
 
AD = 1
BE = 1
AG + CD = 0
AH + BG + CF = 3
BI + CH = 0
CI = -1
 
All those letters are either 1 or -1. If you make A = 1, then a little 
reasoning tells you all the letters are 1 except C and F, which are -1.
 
So the factorization of your equation is 
 
(Ax + By + C)(Dx² + Ey² + Fxy + Gx + Hy + I) = 0
 
becomes
 
(1x + 1y - 1)(1x² + 1y² - 1xy + 1x + 1y + 1) = 0
 
or 
 
(x + y - 1)(x² - xy + x + y² + y + 1) = 0
 
Whew!  Factoring that sure was hard!

We set each factor equal to 0,
 
Setting the first factor = 0,

               x + y - 1 = 0
                   x + y = 1
 
Setting the second factor = 0,
 
 x² - xy + x + y² + y + 1 = 0

y² + (1-x)y + (x²+x+1) = 0
 
Solving for y:

y = 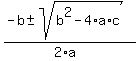%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ 

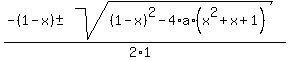y = %28-%281-x%29+%2B-+sqrt%28+%281-x%29%5E2-4%2Aa%2A%28x%5E2%2Bx%2B1%29+%29%29%2F%282%2A1%29+


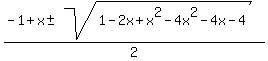y = %28-1%2Bx+%2B-+sqrt%281-2x%2Bx%5E2-4x%5E2-4x-4%29%29%2F2+

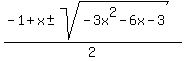y = %28-1%2Bx+%2B-+sqrt%28-3x%5E2-6x-3%29%29%2F2+
 
y = %28-1%2Bx+%2B-+sqrt%28-3%28x%5E2%2B2x%2B1%29+%29%29%2F2+

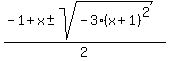y = %28-1%2Bx+%2B-+sqrt%28-3%28x%2B1%29%5E2+%29%29%2F2+

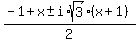y = %28-1%2Bx+%2B-+i%2Asqrt%283%29%28x%2B1%29%29%2F2+

That will be imaginary unless the i-term
is zero.  So we set it = 0

i*sqrt(3)(x+1) = 0
           x+1 = 0 
             x = -1

Then substituting that 

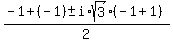y = %28-1%2B%28-1%29+%2B-+i%2Asqrt%283%29%28-1%2B1%29%29%2F2+
   
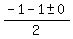y = %28-1-1+%2B-+0%29%2F2+

y = %28-2%29%2F2

y = -1

So we end up with all solutions

{(x,y) | x + y = 1}  plus the one solution (x,y) = (-1,-1)    

Now if you were asking about x+y instead of x-y, the answer would be

x+y is always either 1 or -2.

Are you sure you didn't make a typo and you were asking about x+y and 
not x-y?  That would have made a more interesting problem.

But since you are asking about x-y, then taking the first solution

x + y = 1

let x = integer n:

n + y = 1 

    y = 1 - n

So all those solutions are (x,y) = (n,1-n) 
   
So x-y = n-(1-n) = n-1+n = 2n-1, which can represent any odd number.

So x-y can be any odd number or the one even number 0 when

(x,y) = (-1,-1), for then x-y will be (-1)-(-1) = 0.

Answer:  

x-y can be any odd number or 0.

but x+y can only be 1 or -2

Edwin

Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
From the binomial expansion, we have

, which we can write as

.

Clearly, all (x,y) satisfying x+y = 1 work. Note that the other tutor also stated x+y = 1, using a valid argument, but the solution is much longer.

Now suppose x+y was not equal to 1. We may treat the original equation as a cubic equation by fixing a value for y and solving for x. In other words, we want to find integer roots for the cubic equation

other than x = 1-y.

Here, we use the fact that if r is a root of a polynomial, then 1-r is a factor. We divide both sides by x - (1-y) or x+y-1:

. Solve for x via the quadratic formula.







One thing to note: the expression inside the radical is equal to -3(y+1)^2. Since the square of a number is always non-negative, we will never have a real root, unless the expression inside the radical is equal to zero. Hence, we want y to equal -1. If y = -1, then x is also equal to -1. It is seen that (x,y) = (-1,-1) satisfies the original equation.

Therefore, the only solutions to the original equation are ordered pairs (x,y) satisfying x+y = 1 or (-1,-1). We want to evaluate x-y, which is equal to (x+y)-2y, or 1-2y, which can be any odd number (since y can equal anything). Also, (-1,-1) yields x-y = 0. Hence, the possible values for x-y are odd numbers and 0.