Since you didn't specify which of the many different ways to solve
these, I'll just pick one. If you want it solved by whatever method
you are studying, and this isn't the one, you have to tell us. The
answer is correct, though, regardless of which of the many methods you
are presently studying.
(1) 3x-5y+2z=-12
(2) x+4y-2z= 8
(3) -3x+5y-2z= 12
Multipy (2) through by -3
(4) -3x-12y+6z=-24
Add (4) and (1)
(4) -3x-12y+6z=-24
(1) 3x- 5y+2z=-12
-------------------
(5) -17y+8z=-36
Add (1) and 3):
(1) 3x-5y+2z=-12
(3) -3x+5y-2z= 12
-------------------
(6) 0z= 0
So z can be any number, say
(7) z = a
Substuting (7) in (5)
(5) -17y+8z=-36
-17y+8a=-36
-17y=-36-8a
17y= 36+8a
(8) y=  +
+ a
Substituting (7) and (8) into (2),
(2) x+4y-2z= 8
x+4(
a
Substituting (7) and (8) into (2),
(2) x+4y-2z= 8
x+4( +
+ a)-2(a) = 8
x+
a)-2(a) = 8
x+ +
+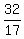 a-2a = 8
Clear of fractions by multiplying through by 17
17x+144+32a-34a = 136
17x+144-2a = 136
17x = 2a-8
x =
a-2a = 8
Clear of fractions by multiplying through by 17
17x+144+32a-34a = 136
17x+144-2a = 136
17x = 2a-8
x = 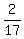 a-
a- Solution: (x, y, z) = (
Solution: (x, y, z) = (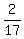 a-
a- ,
,  +
+ a, a)
Edwin
a, a)
Edwin