SOLUTION: Jim's drama teacher randomly chooses 7 students from the class to participate in the class play. if there are 35 students in Jim's drama class, what are his chances of being chosen

If you start with n things, and then you CHOOSE r of them,
the total number of different ways you could choose them 
is written:  

nCr

or

nCr 

or

C(n,r) 

or



The formula is either this



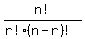or this rule.

If r is larger than half of n, then subtract r from
n and use that as the new value of r.
Now start with n, then multiply that by one less than n,
then by one less than that until you have exactly
r factors.  Put that on top and r! on the bottom of 
the fraction.

---

In your problem, we start with 35 students, then CHOOSE 7,
which is written  

35C7

or

35C7 

or

C(35,7) 

or



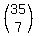I'll use that second rule. 7 is not more than half of n,
so we put 7 factors on top, and 7! on the bottom.  I'll 
start with 35 and come down until I have 7 factors on top. 
Then I'll put 7! on the bottom:



All of the factors on the bottom will cancel into factors 
in the top and you'll end up with 

6,724,520

That's the number of possible different groups of 7 you could
choose from the 35.

Edwin